히스토그램 처리
개요
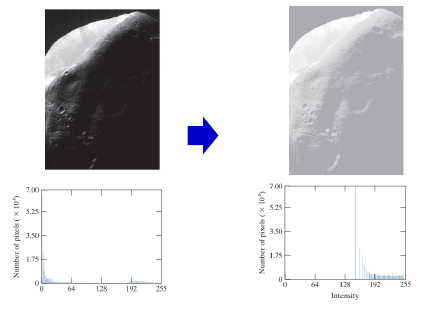
히스토그램 평활화는 이미지의 전반적인 대비를 개선하기 위해 사용되는 방법이라고 지난 시간에 공부하였다. 하지만, 특정 밝기 계급에 픽셀이 지나치게 집중되어 있을 때, 이 방식은 몇 가지 문제점을 초래할 수 있다. 예를 들면, 평활화 후의 이미지에서 나머지 계급의 세부 정보가 손실되거나, 비자연스러운 노이즈나 패턴이 발생할 수 있다.
이러한 한계를 극복하기 위한 방법으로서 지역 히스토그램 처리 방법을 공부해 보겠다. 그리고 이를 이해하기 위해 히스토그램 매칭 또한 공부해 보도록 하겠다. 히스토그램 매칭(Histogram Matching)은 원하는 히스토그램 분포를 가진 참조 이미지를 사용하여, 타겟 이미지의 분포를 조정하는 방법이다. 반면, 지역 히스토그램 처리(Local Histogram Processing)는 이미지의 주변 픽셀들의 평균과 표준편차 같은 정보를 이용해 원하는 부분만 영상 처리를 하는 기법이다.
본문
Histogram Matching
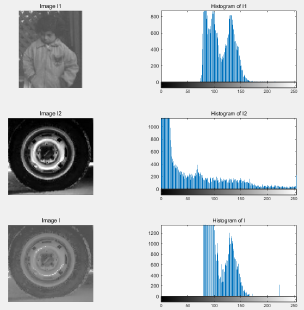
히스토그램 매칭은 입력 이미지에 참조 이미지의 색감을 입히는 기법이다. 이 과정에서 중요한 것은 두 이미지의 히스토그램을 균등한 분포로 만드는 평활화다. 이러한 평활화의 필요성은 주로 세부 정보의 보존 및 데이터 분석의 정확성에서 기인한다.
만약 평활화를 적용하지 않는다면, 이미지의 밝기 분포가 제한된 범위에 집중될 가능성이 있다. 예를 들어, 어두운 환경에서 촬영된 이미지나 부적절한 카메라 설정으로 인해 명암 대비가 낮아진 이미지는 세부 정보를 충분히 반영하지 못하게 된다. 이로 인해 이미지 기반의 데이터 분석에서 원하는 결과를 얻기 어려울 수 있다. 반면 평활화를 사용한다면, 이러한 문제점을 해결하고 이미지의 밝기 분포를 전체 범위에 걸쳐 확장함으로써 이미지의 품질을 향상할 수 있다.
이제 히스토그램 매칭을 진행해 보자. 위에서 언급한 것처럼 입력 이미지 T(밝기 s)와 참조 이미지 G(밝기 z)에 대해 밝기 평활화를 진행하면 다음과 같은 수식을 얻을 수 있다.
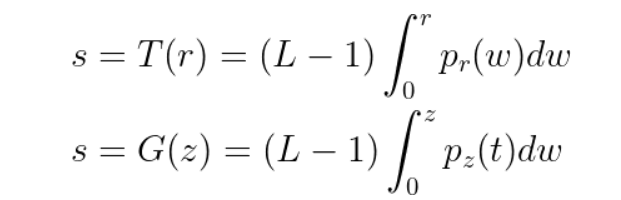
여기서 s는 입력 밝기에 대한 출력 밝기다. 히스토그램 매칭의 목적은 입력 이미지의 히스토그램 T(r)을 참조 이미지의 히스토그램을 G(z)와 동일하게 만드는 것이다. 즉, 입력 이미지의 각 픽셀 값 r에 대한 새로운 픽셀 값이 참조 이미지의 픽셀 값 z의 분포를 따르게 되는 것이다. 따라서 이를 역함수의 관계로 표현하면 다음과 같다.

예를 들어, 타겟 이미지의 밝기 분포가 pr(r), 참조 이미지의 밝기 분포가 pz(z)라고 가정하자. 만약 두 함수가 다음과 같이 표현된다면

각각의 함수에 대해 평활화를 진행하여 z를 구하면 된다. 이를 수식으로 나타내면 다음과 같다.
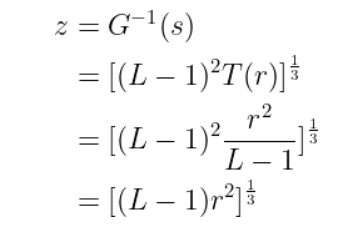
우리가 다루는 이미지는 디지털 형식이므로, 적분 대신 시그마 ∑를 이용해 역함수를 구하면 된다.

매칭 원리
여기서 히스토그램을 매칭할 때 두 이미지의 히스토그램이 비슷하게 조절된다. 하지만 두 이미지의 색상 분포나 밝기 분포가 조절되는 과정에서 이미지의 윤곽은 유지된다. 이는 픽셀 간의 상대적인 관계가 유지되며 그들의 절대적인 값만 바뀌어서 그런 것이다. 즉, 이미지의 픽셀 값들은 변경되지만, 그들 사이의 순서나 대소 관계가 바뀌지 않기 때문이다.

쉽게 이해하기 위해 다음과 같이 두 이미지가 [0 50 ; 200 100], [4 2 ; 0 1]의 픽셀 값을 갖고 있다고 가정해 보자. 이들을 평활화하면 입력 이미지가 참조 이미지의 분포를 따라가므로 다음과 같이 될 것이다.

이처럼 픽셀 값들은 변했지만, 이들 사이의 상대적인 순서(가장 어두운 값, 그다음으로 어두운 값, 가장 밝은 값, 그다음으로 밝은 값)는 유지된다. 즉, 원래 이미지에서 가장 어두운 픽셀은 매칭 후에도 여전히 가장 어두워야 하며, 가장 밝은 픽셀은 여전히 가장 밝다. 이러한 상대적인 순서의 유지는 이미지의 외형적인 특성, 윤곽선, 패턴 등을 보존하게 해 준다.
구현

왼쪽에 있는 이미지를 입력으로, 오른쪽에 있는 이미지를 참조 이미지라고 해보자. 참조 이미지의 색감을 입력 이미지에 씌우는 것을 목표로 하고, Gray Level일 때와 Color Level 일 때 모두 다뤄보겠다.
RGB to RGB

Iin = imread("histo_match_example1.jpg");
Iref = imread("histo_match_example2.jpg");
Ires = imhistmatch(Iin, Iref, 256);
figure(1);
subplot(3,2,1); imshow(Iin); title("input");
subplot(3,2,2); imhist(Iin);
subplot(3,2,3); imshow(Iref); title("reference");
subplot(3,2,4); imhist(Iref);
subplot(3,2,5); imshow(Ires); title("result");
subplot(3,2,6); imhist(Ires);
매트랩에서는 히스토그램 매칭을 위해 imhistmatch() 함수를 지원한다. 함수의 첫 번째 인자를 입력으로, 두 번째 인자를 참조로 받았을 때, 첫 번째 인자에 참조 이미지의 히스토그램을 따라가게 매칭시켜 준다.
Gray to RGB
Iin = rgb2gray(imread("histo_match_example1.jpg"));
Iref = imread("histo_match_example2.jpg");
R_ch = imhistmatch(Iin, Iref(:,:,1), 256);
G_ch = imhistmatch(Iin, Iref(:,:,2), 256);
B_ch = imhistmatch(Iin, Iref(:,:,3), 256);
Ires = cat(3, R_ch, G_ch, B_ch);
figure(1);
subplot(3,2,1); imshow(Iin); title("input");
subplot(3,2,2); imhist(Iin);
subplot(3,2,3); imshow(Iref); title("reference");
subplot(3,2,4); imhist(Iref);
subplot(3,2,5); imshow(Ires); title("result");
subplot(3,2,6); imhist(Ires);
Gray 이미지는 N*M*1, RGB 이미지는 N*M*3이므로 Gray 이미지의 채널을 3개 늘려줘야 한다. 즉, RGB의 채널과 Gray 이미지를 각각 히스토그램 매칭을 진행해줘야 한다. 그렇지 않으면 다음과 같은 에러가 발생한다.

'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Spatial Filtering (1) (2) | 2023.11.02 |
|---|---|
| [디지털영상처리] Histogram Processing (2) (0) | 2023.10.17 |
| [디지털영상처리] Histogram Equalization (2) (0) | 2023.10.13 |
| [디지털영상처리] Histogram Equalization (1) (0) | 2023.10.12 |
| [디지털영상처리] Intensity Transformation(2) (2) | 2023.10.08 |