본문
Histogram Equalization

히스토그램 평활화(Histogram Equalization)는 이미지의 밝기 분포를 균등하게 재분배함으로써 대비를 개선하는 기법이다. 이 과정에서 각 픽셀의 밝기 값을 조정하되, 이미지의 해상도는 그대로 유지한다. 따라서, 원본 이미지의 모든 픽셀은 보존되며, 그저 픽셀들의 밝기가 재조정되어 이미지의 대비와 세부 정보가 강화된다. 이를 수식으로 나타내면 다음과 같다.

따라서 히스토그램 평활화의 목표는 가능한 어떤 이미지라도 모든 밝기 레벨을 동적 범위(이미지에서 나타날 수 있는 최소 밝기와 최대 밝기 사이의 범위) 내에서 균등하게 사용하여, 이미지의 대비를 개선하는 것이다. 이 과정에서 원하지 않는 노이즈와 같은 아티팩트(Artifacts)들이 생길 수 있고, 픽셀의 분포에서 밝기가 역전되면 안 된다.
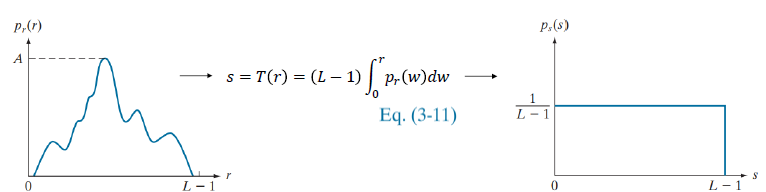
다음과 같은 분포를 가진 단조 증가(Strictly Monotonicaaly) PDF 함수가 있다고 가정해 보자. 히스토그램은 결국 0부터 L까지의 밝기 분포를 나타내는 함수이므로 이를 확률 밀도 함수로 나타내면 위의 적분식처럼 변형된다. 그리고 함수의 넓이는 1이 되어야 한다(0부터 L-1까지의 빈도가 나타날 확률은 1이 되어야 함). 우리의 목표는 이러한 빈도수를 1/(L-1)로 평평하게 맞추는 것이다.
예를 들어 pr(r) 함수에서 r = 0부터 r = 100까지의 넓이(적분 값)가 0.2라고 가정해 보자. 이는 원본 이미지에서 픽셀 강도가 100 이하일 확률이 20%라는 의미다. 따라서 s = T(100) = 255 * 0.2 = 51이 되어야 한다. 이때 ps(s)는 s와 r 사이의 관계를 파악한 후에 다음과 같은 공식으로 1/(L-1)라는 값으로 계산된다.

즉, 원래의 히스토그램의 형태에 상관없이 항상 균일한 분포(Uniform distribution)를 띄워야 한다.
이번에는 pr(r) = 2r/(L-1)^2 ( 0 ≤ r ≤ L-1 )의 PDF 함수를 평활화하는 T(r) 함수를 찾아보자. 이를 수식으로 풀면 다음과 같은 결과를 얻을 수 있다.
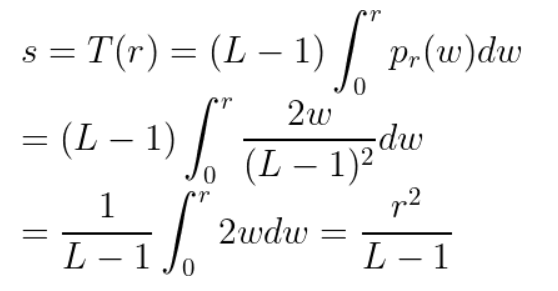
하지만 우리가 다루는 것은 디지털 이미지기 때문에, 연속적인 함수에 대한 적분이 아닌, 불연속적(Discreted)인 함수에 대한 합(Sigma)을 계산해야 한다. 따라서 이를 수식으로 나타내면 다음과 같다.
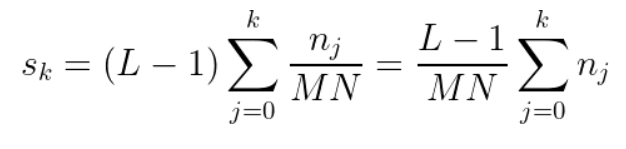
즉, 해당 과정을 요약하면 다음과 같다.
- 히스토그램 계산: 이미지의 히스토그램 pr(r)을 계산
- CDF 계산: 원래 이미지의 누적 분포 함수 T(r)을 계산
- 픽셀 값 업데이트: 각 픽셀의 값 r을 새로운 값 s로 변환
구현
function h = Myhist(Ig, L)
h = zeros(L, 1);
[M,N] = size(Ig);
for i = 1:M
for j = 1:N
h(Ig(i,j) + 1) = h(Ig(i,j) + 1) + 1;
end
end
endMyhist()는 히스토그램을 생성하는 함수로, x축은 계급을, y축은 빈도를 나타낸다. L * 1 크기의 빈 배열을 초기화한 후, 각 빈도에 해당하는 영역을 업데이트한다. 즉, 이 함수는 히스토그램 분포를 생성하는 단계를 담당한다.
function Ieq = Myhisteq(Ig, L)
[M,N] = size(Ig);
Ieq = zeros(M,N);
hist = Myhist(Ig, L);
cdf = zeros(L, 1);
cdf(1) = hist(1);
for i = 2:L
cdf(i) = cdf(i - 1) + hist(i);
end
cdf = (L-1)/(M*N) * cdf;
for i = 1:M
for j = 1:N
Ieq(i,j) = round(cdf(Ig(i,j) + 1));
end
end
Ieq = uint8(Ieq);
endMyhisteq()는 이미지 배열에 평활화를 적용하는 함수다. 앞서 언급된 히스토그램 평활화 과정에 따라, 먼저 누적분포함수 cdf를 계산한다. 이를 위해 루프를 사용하여, 각 레벨에서의 누적 확률을 계산하고, 상수를 사용해 [0 L-1] 범위로 정규화한다. 마지막으로 평활화된 이미지 Ieq를 생성하고, 디지털 이미지에 맞게 uint8로 자료형을 변환해 주었다.

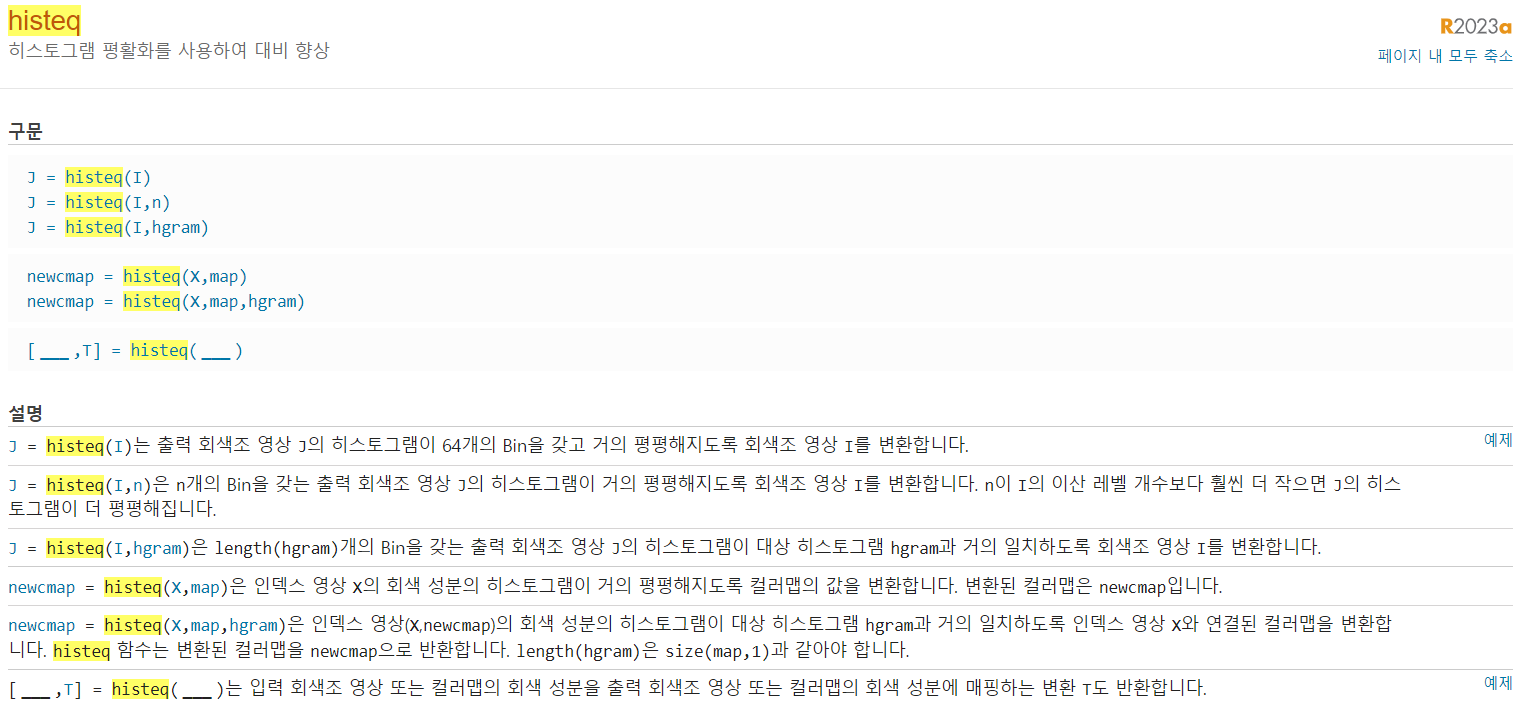
매트랩에서는 히스토그램 분석을 지원하는 다양한 함수들이 존재한다. 대표적으로 히스토그램을 계산해서 계급과 빈도수를 반환하는 imhist() 함수, 이미지 배열을 평활화해 주는 histeq() 함수가 있다. 이 함수들을 이용해서 히스토그램 평활화를 해서 앞에서 구현한 함수와 비교해 보도록 하자.
Ig = rgb2gray(imread('example.jpg'));
[M,N] = size(Ig);
h1 = imhist(Ig, 256);
h1 = h1 / (M*N);원본 이미지 Ig에 대한 히스토그램 분포를 계산해 보자. 이미지를 불러온 후, imhist() 함수를 이용해 이미지의 히스토그램 분포를 h1에 초기화한다. 이때 확률 분포로 표현하기 위해 크기 M*N으로 나눠주었다.
Ieq = histeq(Ig, 256);
h2 = imhist(Ieq, 256);
h2 = h2 / (M*N);원본 이미지에 평활화를 적용하기 위해 histeq() 함수를 이용해 Ieq를 초기화하였다. 그리고 이 배열의 히스토그램 분포를 확인하기 위해 imhist() 함수를 사용해 h2에 할당하였다.
Ieq_my = Myhisteq(Ig, 256);
h3 = Myhist(Ieq_my, 256);
h3 = h3 / (M*N);
figure(1);
subplot(3,2,1); imshow(Ig); title("Original image");
subplot(3,2,2); bar(h1); title("Original image histogram");
subplot(3,2,3); imshow(Ieq); title("Equalization image");
subplot(3,2,4); bar(h2); title("Equalization image histogram");
subplot(3,2,5); imshow(Ieq_my); title("Myhist image");
subplot(3,2,6); bar(h3); title("Myhisteq image equalization");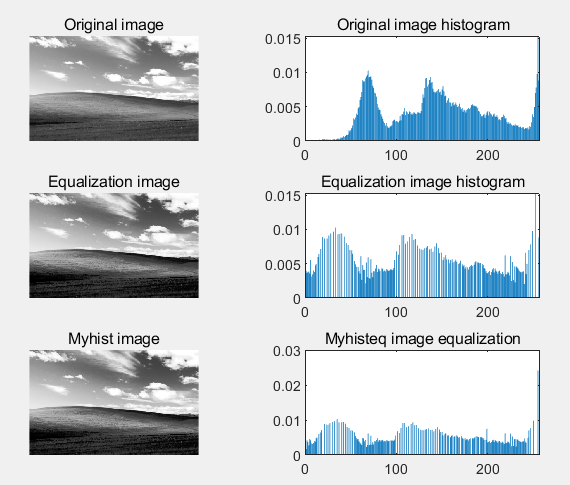
평활화를 진행한 이미지 배열의 분포가 생각보다 균일하지 않다. 이 이유는 여러 가지다. 이미지 자체가 대부분의 영역에서 균일한 밝기 분포를 갖고 있거나, 이미지의 특정 영역이나 픽셀 값들이 다른 영역에 비해 독보적으로 많이 분포해 있어, 평활화가 완전히 이루어지지 않을 수 있다. 즉, 일부 세부 정보가 손실될 수 있다는 것이다. 해당 이미지의 경우 중간 밝기 값 주변과 끝 쪽 밝기 주변에 높은 빈도가 있어, 평활화에 영향을 끼친 것으로 예측된다.
총합본
Ig = rgb2gray(imread('example.jpg'));
[M,N] = size(Ig);
h1 = imhist(Ig, 256);
h1 = h1 / (M*N);
Ieq = histeq(Ig, 256);
h2 = imhist(Ieq, 256);
h2 = h2 / (M*N);
Ieq_my = Myhisteq(Ig, 256);
h3 = Myhist(Ieq_my, 256);
h3 = h3 / (M*N);
figure(1);
subplot(3,2,1); imshow(Ig); title("Original image");
subplot(3,2,2); bar(h1); title("Original image histogram");
subplot(3,2,3); imshow(Ieq); title("Equalization image");
subplot(3,2,4); bar(h2); title("Equalization image histogram");
subplot(3,2,5); imshow(Ieq_my); title("Myhist image");
subplot(3,2,6); bar(h3); title("Myhisteq image equalization");
function h = Myhist(Ig, L)
h = zeros(L, 1);
[M,N] = size(Ig);
for i = 1:M
for j = 1:N
h(Ig(i,j) + 1) = h(Ig(i,j) + 1) + 1;
end
end
end
function Ieq = Myhisteq(Ig, L)
[M,N] = size(Ig);
Ieq = zeros(M,N);
hist = Myhist(Ig, L);
cdf = zeros(L, 1);
cdf(1) = hist(1);
for i = 2:L
cdf(i) = cdf(i - 1) + hist(i);
end
cdf = (L-1)/(M*N) * cdf;
for i = 1:M
for j = 1:N
Ieq(i,j) = round(cdf(Ig(i,j) + 1));
end
end
Ieq = uint8(Ieq);
end요약
히스토그램
1. 정의: 데이터의 분포를 그래프 형태로 시각화한 것으로, 디지털 영상 처리 관점에서는 각 픽셀 값의 등장 빈도를 표현
2. 특징
a. 이미지의 대비 혹은 밝기가 변하면, 히스토그램이 바뀜
b. 히스토그램이 어두우면 그래프가 왼쪽으로, 밝으면 오른쪽으로, 대비가 낮으면 중앙에 몰림
3. 평활화
a. 정의: 이미지의 밝기 분포를 균등하게 재분배함으로써 대비를 개선하는 기법
b. 과정: 히스토그램 분포 생성 → CDF 계산 → 픽셀 값 업데이트
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Histogram Processing (2) (0) | 2023.10.17 |
|---|---|
| [디지털영상처리] Histogram Processing (1) (2) | 2023.10.16 |
| [디지털영상처리] Histogram Equalization (1) (0) | 2023.10.12 |
| [디지털영상처리] Intensity Transformation(2) (2) | 2023.10.08 |
| [디지털영상처리] Intensity Transformation(1) (2) | 2023.10.07 |