강도 변환
개요

디지털 영상 처리 분야에서, 영상 정보는 주로 변환 도메인(Transform Domain)과 공간 도메인(Spatial Domain)과 에서 표현하고 처리한다. 전자는 이미지를 다른 형태로 변환시켜 나타내는 방식을 의미한다. 예를 들어, 푸리에 변환(Fourier Transform)이나 웨이블릿 변환(Wavelet Transform)과 같은 기법들이 이에 포함된다. 이 도메인에서의 처리는 주로 신호의 주파수 성분을 분석하고 조작하는 데 사용된다.
반면 공간 도메인은 이미지 평면(혹은 이미지 그 자체)에서 픽셀들의 직접적인 밝기 값을 다루고 조작한다. (x, y) 주변의 픽셀 값을 이용해 새로운 g(x, y)를 생성한다는 측면에서 필터링과 비슷한 성격을 띠고 있다. 이를 수식으로 표현하면 다음과 같다.

- f(x, y): input image
- g(x, y): output image
- T: operator on f defined over a neighborhood of point (x, y)
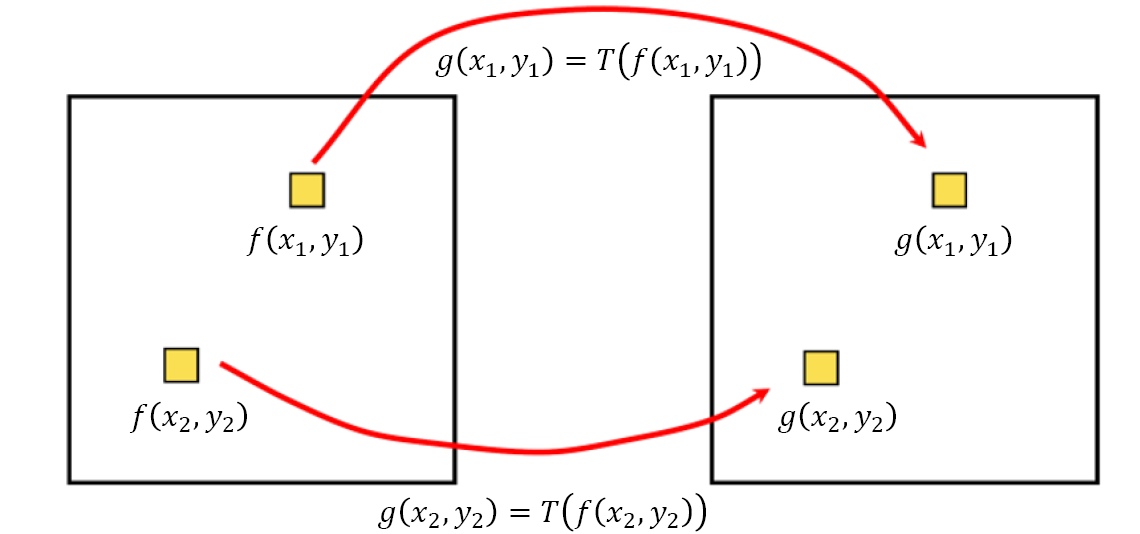
이중, 각 픽셀을 독립적(neighborhood size = 1 x 1)으로 다루는 변환을 강도 변환(Intensity Transformation)이라고 한다. 즉, 출력이 입력의 단일 픽셀의 밝기 값 f(x, y)에만 의존하며, 이를 변형하는 기술을 의미한다. 오늘은 강도 변환의 여러 종류에 대해 알아보고 실습하는 시간을 가지도록 해보자.
본문
Linear Intensity Transformation
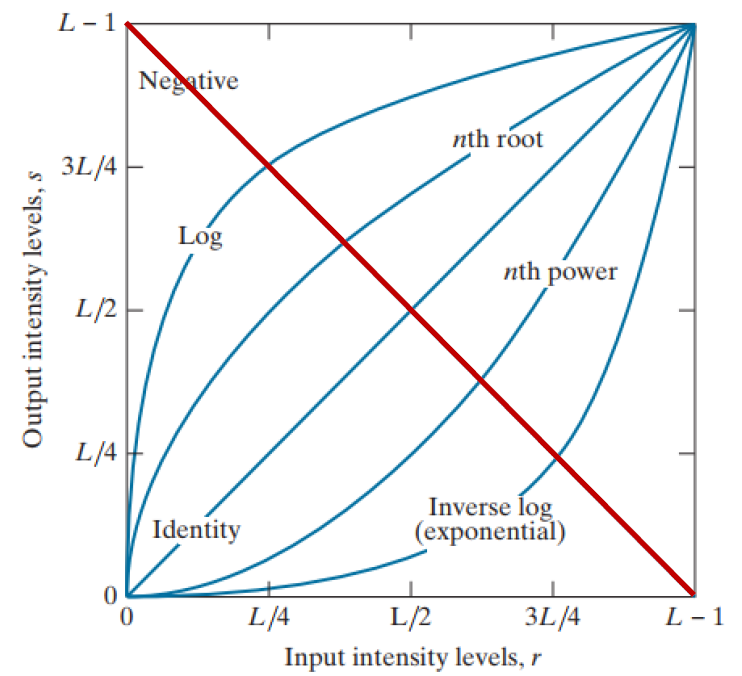
먼저 가장 간단한 밝기 변환인 선형 강도 변환에 대해 알아보자. 이를 크게 두 종류로 나뉠 수 있는데, 밝기를 반전시키는 반전(Negative) 변환과 이미지를 그대로 유지하는 항등(Identity) 변환이 있다. 이를 수식으로 나타내면 다음과 같다.
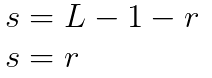
여기서 L은 강도 레벨의 수를 의미하는데, 쉽게 생각해서 L - 1이 절편이고, r이 기울기라고 생각하면 된다. 항등 변환은 따로 건드릴 건 없으니, 반전 변환을 구현해 보도록 하자.

Ig = rgb2gray((imread("example.jpg")));다음과 같은 사진이 있다고 했을 때, 해당 사진을 반전시키려면 어떻게 해야 할까?
In = 256 - 1 - Ig;
figure(1);
subplot(1,2,1); imshow(Ig, []); title("Original");
subplot(1,2,2); imshow(In, []); title("Negative");
위의 수식에서 L은 강도 레벨을 의미하는데, 일반적으로 디지털 이미지는 8 bit(0~255)를 사용하므로 s = 256 - 1 - Ig가 된다. 혹은 매트랩에서 제공하는 이미지 반전 함수인 imcomplement()를 사용해도 된다. 이 함수는 이미지의 보수를 계산해 영상의 색을 반전시킨 후 반환한다.
Log Intensity Transformation
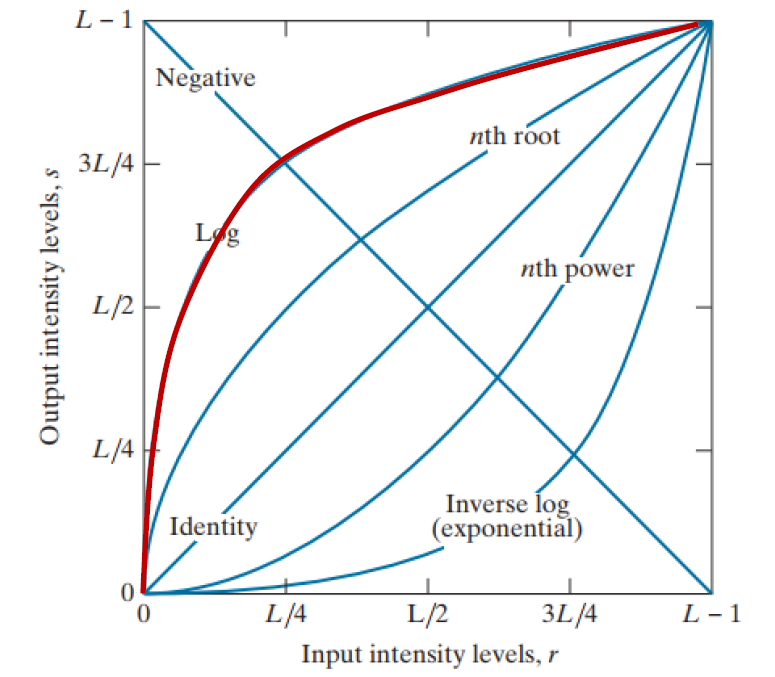
다음은 입력에 로그를 씌워 어두웠던 부분(감마 광도 영역)을 확장하고, 동시에 픽셀 강도의 고조파(Harmonics, 이미지의 경계나 빠르게 변하는 강도의 변화를 나타내는 고주파 성분)를 강조하는 로그 변환이다. 빨간색으로 나타낸 그래프를 보면, 낮은 강도의 픽셀 값에 대해 출력 강도를 크게 증가시키고, 높은 강도의 픽셀 값에 대해서는 상대적으로 적게 증가시킨다.
이를 수식으로 나타내면 다음과 같다.

여기서 c는 강도를 조절하는 스케일 상수이며, 로그 안에 1을 더해준 이유는 r이 0일 때 함수가 발산하는 것을 방지하기 위해서이다.
Ig = rgb2gray((imread("example.jpg")));
c = 2;
Ilog = c * log(1 + double(Ig));
figure(1);
subplot(1,2,1); imshow(Ig, []); title("Original");
subplot(1,2,2); imshow(uint8(Ilog), []); title("Log");
여기서 주목해야 할 것은 형변환이다. 로그 변환을 적용할 때, 로그 안의 인자는 실수형이어야 한다. 하지만 이미지 값은 음이 아닌 8비트 정수이므로 반드시 형변환을 적용시켜줘야 한다. 그리고 이미지를 출력하는 imshow() 함수는 인자로 uint8을 받아야 하므로, double형인 Ilog 변수를 해당 자료형으로 바꿔줘야 한다. 그렇지 않으면 다음과 같이 에러가 발생하게 된다.

Power-Law(Gamma) Intensity Transform
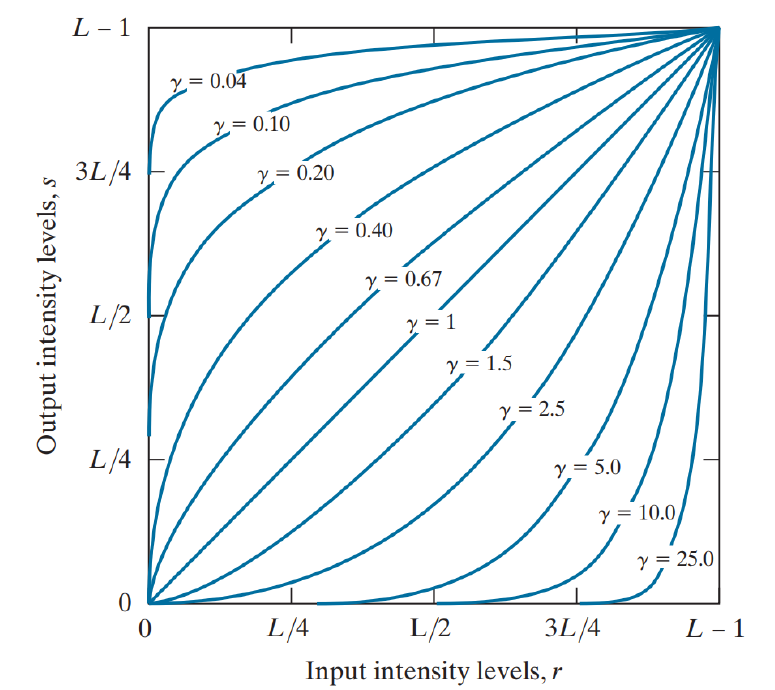
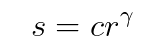
그리고 영상의 전체적인 명암 대비를 조절하고, 특히 어두운 영역의 세부 정보를 향상하는 데 주로 사용하는 감마 변환(Power-Law, Gamma Transformaiton)이 있다. 감마 변환은 보정된 영상이 인간의 시각 체계와 더 잘 부합하도록 영상의 강도를 수정한다. 즉, 비선형적인 왜곡을 선형적으로 역보상해 준다. 이는 인간의 시각 체계가 선형적이지 않은 것에서 기인하는데, 원론적인 이야기이므로 궁금하다면 아래의 접은 글을 확인해 보면 된다.
인간의 시각 체계는 선형적이지 않다. 다시 말해, 우리의 눈은 영상의 모든 밝기 레벨을 동일하게 인지하지 않는다. 오히려 인간의 시각은 어두운 영역에 민감하며, 밝은 영역에 대해서는 상대적으로 둔감하다(웹버-페허의 법칙).
이런 인간의 시각 특성으로 인해, 선형적인 밝기 변환은 우리 눈에 동일하게 인식되지 않는다. 예를 들어, 어두운 그림자 부분에서 약간의 밝기 증가는 눈에 뚜렷하게 느껴지지만, 이미 밝은 영역에서 같은 밝기 변화는 거의 눈에 띄지 않는다.
감마 보정은 이러한 인간의 비선형적인 밝기 인지 특성을 보완한다. 감마 변환을 통해 영상의 밝기 레벨을 조절하면, 인간의 눈이 각 밝기 레벨을 더 균등하게 인식할 수 있다. 즉, 감마 보정은 영상의 밝기 분포를 인간의 시각 특성에 맞게 수정하여, 어두운 영역과 밝은 영역에서 세부 정보가 동일하게 눈에 띄도록 만들어준다.
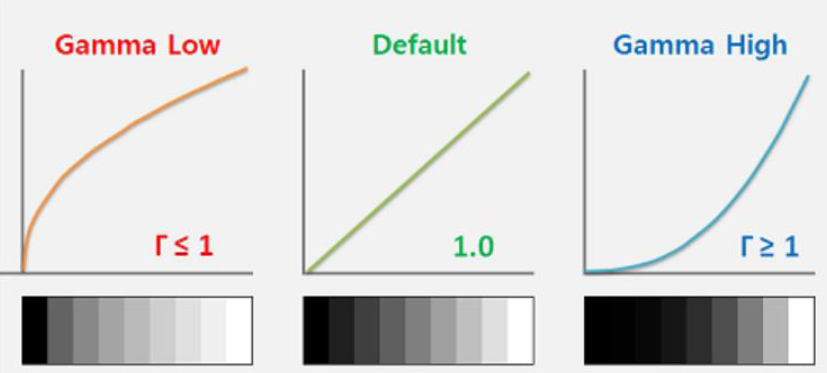
즉, 해당 그래프를 보면 감마 값을 1을 기준으로 입력을 더 밝게(1보다 작은 경우) 할 것인지, 어둡게(1보다 큰 경우) 할 것인지 정할 수 있다는 사실을 알 수 있다. 이번엔 해당 사실을 가시적으로 확인하기 위해 다음과 같이 코드를 짜보았다.
Ig = rgb2gray((imread("example.jpg")));
r1 = 0.5;
r2 = 1;
r3 = 1.5;
Ir1 = double(Ig).^r1;
Ir2 = double(Ig).^r2;
Ir3 = double(Ig).^r3;
figure(1);
imshow(Ig, []); title("Original");
figure(2);
subplot(1,3,1); imshow(Ir1, []); title("r = 0.5")
subplot(1,3,2); imshow(Ir2, []); title("r = 1")
subplot(1,3,3); imshow(Ir3, []); title("r = 1.5")
fprintf("Ig: %.2f\n", mean(Ig, 'all'));
fprintf("Ir1: %.2f\n", mean(Ir1, 'all'));
fprintf("Ir2: %.2f\n", mean(Ir2, 'all'));
fprintf("Ir3: %.2f\n", mean(Ir3, 'all'));
흑백 이미지의 평균 밝기 값이 122.96일 때, 감마 값이 1보다 작은 경우 (예: Ir1) 이미지는 원본보다 밝아져야 하며, 감마 값이 1보다 큰 경우 (예: Ir3)는 원본보다 어두워져야 한다. 그러나 감마 변환을 진행하며 발생하는 거듭제곱 연산(double.^)으로 인해 이미지의 픽셀 값들이 큰 폭으로 변하게 되어, 평균 밝기 값 또한 크게 튀는 현상을 볼 수 있다. 이를 해결하기 위해서는 감마 변환 후의 이미지 값을 적절한 범위로, 예를 들면 [0, 255]로 정규화하는 과정이 필요하다. 정규식은 다음과 같다.

Ig = rgb2gray((imread("example.jpg")));
r1 = 0.5;
r2 = 1;
r3 = 1.5;
Ir1 = double(Ig).^r1;
Ir2 = double(Ig).^r2;
Ir3 = double(Ig).^r3;
figure(1);
imshow(Ig, []); title("Original");
Ir1 = (Ir1 - min(Ir1(:))) / (max(Ir1(:)) - min(Ir1(:))) * 255;
Ir2 = (Ir2 - min(Ir2(:))) / (max(Ir2(:)) - min(Ir2(:))) * 255;
Ir3 = (Ir3 - min(Ir3(:))) / (max(Ir3(:)) - min(Ir3(:))) * 255;
figure(2);
subplot(1,3,1); imshow(uint8(Ir1), []); title("r = 0.5")
subplot(1,3,2); imshow(uint8(Ir2), []); title("r = 1")
subplot(1,3,3); imshow(uint8(Ir3), []); title("r = 1.5")
fprintf("Ig: %.2f\n", mean(Ig, 'all'));
fprintf("Ir1: %.2f\n", mean(Ir1, 'all'));
fprintf("Ir2: %.2f\n", mean(Ir2, 'all'));
fprintf("Ir3: %.2f\n", mean(Ir3, 'all'));
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Histogram Equalization (2) (0) | 2023.10.13 |
|---|---|
| [디지털영상처리] Histogram Equalization (1) (0) | 2023.10.12 |
| [디지털영상처리] Intensity Transformation(2) (2) | 2023.10.08 |
| [디지털영상처리] Resolution (2) | 2023.10.03 |
| [디지털영상처리] 개요 (0) | 2023.09.29 |