필터
개요

디지털 영상 처리 관점에서 필터(Fliter)는 이미지의 특정 정보를 강조하거나, 불필요한 정보를 제거하여 이미지의 품질을 개선하는 데 사용되는 기술이나 알고리즘을 의미한다. 우리가 스마트폰으로 사진을 찍을 때 사용하는 카메라 어플도 필터의 일종이다. 예를 들어, 이미지의 전반적인 색온도를 증가시키면 따뜻한 느낌으로 변한다. 이러한 필터는 공간적 필터와 주파수 필터(Frequency Filter)로 나눌 수 있는데, 이번 시간에는 공간적 필터의 일종인 선형 필터 중 합성곱(Convolution)과 상관분석(Correlation)에 대해 알아보자.
본문
공간 필터와 Corrleation, Convolution

공간 필터(Spatial Filter)는 이미지의 각 픽셀과 그 주변 픽셀들에 수학적 연산을 적용하여 새로운 이미지를 생성하는 과정이다. 픽셀 값에 어떤 연산을 한다는 관점에서 앞서 배웠던 밝기 변환(Intensity Transform)과 비슷하다고 할 수 있지만, 후자는 개별 픽셀에만 영향을 미친다는 차이가 있다. 이 과정은 일반적으로 특정 크기의 커널(혹은 마스크)을 사용하며, 이 커널이 이미지 위를 이동하면서(Sliding) 각 픽셀에 대해 연산을 수행한다. 이때 사용하는 커널의 종류는 크게 컨볼루션과 상관관계가 있다.
먼저 컨볼루션(Convolution)은 입력 이미지와 컨볼루션 커널 간 요소별 곱셈과 합을 통해 수행한다. 즉, 커널을 이미지 위에 겹쳐 놓고, 커널과 겹치는 이미지 부분의 각 픽셀과 커널의 해당 값과의 곱을 모두 더해서 새로운 이미지의 픽셀 값을 생성한다. 이때 컨볼루션은 커널을 이미지에 적용하기 전, 수평과 수직으로 뒤집는다. 이는 신호 처리에서 두 함수의 컨볼루션이라는 수학적 개념에서 유래한 것으로, 수식으로 나타내면 다음과 같다.

반면 상관관계(Corrleation)는 컨볼루션과 매우 비슷하지만, 커널을 뒤집지 않고 직접 적용한다. 상관관계 연산에서는 커널과 이미지의 겹치는 부분에서 요소별 곱셉을 수행하고, 그 결과를 모두 합산하여 새로운 이미지를 생성한다. 이를 수식으로 나타내면 다음과 같다.

위의 수식들을 이해하기 위해 다음과 같은 이미지 배열의 일부와 커널이 있다고 가정해 보자.

먼저 해당 배열에 커널을 Convolutin을 이용해 Sliding을 해보자. Convolution은 커널을 먼저 수평과 수직으로 뒤집은 다음 배열에 적용해야 하므로 다음과 같이 계산된다.

Correlation을 이용해 Sliding을 하면 다음과 같이 계산된다.

Cross Correlation

앞서 설명한 상관관계는 필터를 이미지에 슬라이딩했을 때, 유사한 부분에서 높은 값이 출력된다. 이는 요소별 곱셉을 진행할 때, 유사한 값끼리 곱하면 큰 값이 나오고, 불일치하는 부분에서는 작은 값이나 음수가 나오는 것에서 기인한다. 이를 이용해 이미지에서 어떤 패턴, 특징 또는 템플릿과 일치하는 부분을 찾는 데 사용할 수 있다.

이러한 특징을 이용한 것이 교차 상관관계(Cross Correlation)다. 하지만 이러한 방식에는 한 가지 문제점이 있다. 만약 입력 이미지에 큰 수가 있는 경우, 유사도와 별개로 큰 값이 출력된다. 이는 Cross Correlation의 선형적인 특성 때문인데, 이로 인해 해당 영역이 템플릿과 유사하다는 것을 반드시 의미하는 것이 아니게 된다.

예를 들어, 왼쪽과 같은 이미지에 두 부분을 오른쪽 템플릿을 씌운다고 해보자.

그 결과, 유사도가 떨어지는 왼쪽의 이미지 배열이 더 큰 값을 갖게 된다. 이로 인해 Cross Correlation은 절대적인 밝기 값의 변화에 매우 민감하게 반응하며, 이는 이미지의 다른 부분에서도 비슷한 밝기 수준의 픽셀이 존재한다면, 실제 구조나 패턴과 관계없이 높은 상관 값을 생성하게 된다.
이를 해결하기 위해 각 신호의 평균을 빼고 표준 편차로 나누어 신호를 정규화한 정규화 교차 상관관계(Normalized Cross Correlation, NCC)를 사용한다. 이렇게 함으로써 신호의 강도와 분산을 표준화하여, 신호의 절대적인 값 대신 구조의 패턴의 유사성을 비교하는 데 초점을 맞출 수 있다.
I1 = [5 2 1; 1 0 0; 1 0 0];
I2 = [1 1 1; 0 0 1; 0 0 1];
It = [1 1 1; 0 0 1; 0 0 1];
I1n = (I1 - mean(I1, 'all')) / std(I1, 1, 'all');
I2n = (I2 - mean(I2, 'all')) / std(I2, 1, 'all');
Itn = (It - mean(It, 'all')) / std(It, 1, 'all');
corr2(I1, It)
corr2(I2, It)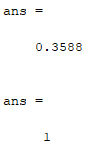
이렇게 직접 정규화하지 않고 매트랩에서 제공하는 normxcorr2를 사용하면 더 쉽게 계산할 수 있다.
I1 = [5 2 1; 1 0 0; 1 0 0];
I2 = [1 1 1; 0 0 1; 0 0 1];
It = [1 1 1; 0 0 1; 0 0 1];
res1 = normxcorr2(I1, It);
res2 = normxcorr2(I2, It);
max(res1(:))
max(res2(:))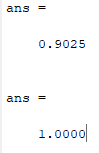
요약
공간 필터
1. 정의: 이미지의 각 픽셀과 그 주변 픽셀들에 수학적 연산을 적용하여 새로운 이미지를 생성하는 과정
2. 종류(선형 필터)
a. 컨볼루션: 입력 이미지를 180도 회전시키고 요소별 곱셈 후 합을 하는 방법
b. 상관관계: 입력 이미지 그대로 요소별 곱셈 후 합을 하는 방법
3. 교차 상관관계
a. 정의: 입력 이미지와 템플릿의 유사성을 측정
b. 단점: 큰 수가 곱해질 때 결과적으로 높은 유사도를 출력한다는 문제점
c. 정규화 교차 상관관계: 교차 상관관계의 문제를 정규화함으로써 해결
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Image Sharpening (1) (0) | 2023.11.06 |
|---|---|
| [디지털영상처리] Smoothing Spatial Filtering (0) | 2023.11.05 |
| [디지털영상처리] Histogram Processing (2) (0) | 2023.10.17 |
| [디지털영상처리] Histogram Processing (1) (2) | 2023.10.16 |
| [디지털영상처리] Histogram Equalization (2) (0) | 2023.10.13 |