Smoothing
개요
지난 시간에는 이미지에 Correlation를 이용해 필터를 씌우는 방법에 대해 배워봤다. 이번 시간에는 이를 이용해 이미지를 부드럽게 만드는 스무딩 필터에 대해 알아보자.
본문
Linear Smoothing Spatial Filter

스무딩 공간 필터(Smoothing Spatial Filter)는 이미지의 노이즈를 감소시키고, 세부 사항을 부드럽게 처리하여 전반적인 블러링(Blurring) 효과를 제공하는 데 사용된다. 이 필터는 이미지의 선명도를 다소 감소시키는 대신 노이즈를 줄이는 역할을 하며, 선형 필터와 비선형 필터로 나눌 수 있다. 이때 부드럽게 만드는 원리는 이미지의 작은 디테일들을 지우고, 지운 공간을 연결하는 것이다. 즉, 사라진 픽셀의 값을 가중치 필터를 이용하여 픽셀의 값을 그 주변 픽셀 값들로 적절히 조정하는 것이다.
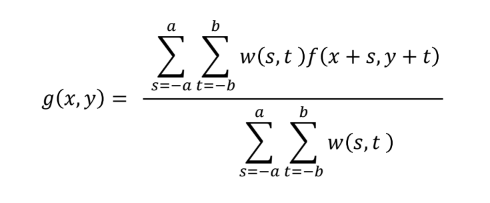
선형 스무딩 필터는 이미지의 각 픽셀 값을 해당 픽셀의 주변 픽셀 값들과 평균을 내 부드럽게 만든다. 이 과정에서 correlation 연산을 사용하여 이미지의 각 픽셀에 마스크를 적용하고, 각 위치에서 마스크의 가중치와 이미지 픽셀 값을 곱한 후 총합을 새로운 픽셀 값으로 설정한다. 마스크의 가중치는 필터링 효과를 결정하며, 성능은 가중치 설정에 크게 의존한다.
평균 필터를 예로 들면, 이 필터는 모든 가중치 w(s,t)가 같고 1인 경우를 말한다. 3x3 마스크를 사용한다고 할 때, 각 가중치에 대한 합은 다음과 같다.

이 합은 이미지의 각 픽셀 값에 대한 총합을 나누어 평균값을 계산하는 데 사용된다. 따라서 평균 필터의 마스크는 다음과 같이 표현된다.

이 마스크를 적용하면, 이미지의 각 픽셀은 자신을 포함한 주변 9개 픽셀의 평균값을 취하게 되어, 노이즈가 감소하고 이미지가 부드럽게 처리된다. 이러한 평균화 과정은 세부 사항을 줄이는 대신 이미지를 부드럽게 만드는 데 도움이 될 수 있다.
I = imread("example2.jpg");
n = randn(size(I)) * 20;
In = uint8(double(I) + n);

원본에 가우시안 노이즈가 추가된 이미지를 평균 가중치를 이용한 스무딩 필터를 사용해 부드럽게 만들어 보자. 이때 매트랩에서 제공하는 이미지에 필터를 씌우는 imfilter() 함수를 사용하였다.
w1 = ones(1,1) ./ 1;
w2 = ones(5,5) ./ 25;
w3 = ones(10,10) ./ 100;
Ir1 = imfilter(In, w1);
Ir2 = imfilter(In, w2);
Ir3 = imfilter(In, w3);
figure(1);
subplot(1,3,1); imshow(Ir1);
subplot(1,3,2); imshow(Ir2);
subplot(1,3,3); imshow(Ir3);
왼쪽부터 차례대로 평균 가중치 필터의 크기가 1x1, 5x5, 10x10이다. 필터의 크기가 너무 작은 경우 아무런 스무딩 효과가 일어나지 않고, 크기가 커질수록 이미지가 부드러워지는 대신 선명도가 떨어지는 단점이 있었다.
fprintf("Ir1: %.2f\n", mean(Ir1(:)));
fprintf("Ir2: %.2f\n", mean(Ir2(:)));
fprintf("Ir3: %.2f\n", mean(Ir3(:)));
figure(2);
subplot(1,3,1); imhist(Ir1);
subplot(1,3,2); imhist(Ir2);
subplot(1,3,3); imhist(Ir3);
fprintf("Ir1: %.2f\n", std(double(Ir1(:))));
fprintf("Ir2: %.2f\n", std(double(Ir2(:))));
fprintf("Ir3: %.2f\n", std(double(Ir3(:))));
이번에는 이미지에 필터를 씌웠을 때 평균과 표준 편차의 변화와 히스토그램 분포를 관찰해 보자. 각 이미지에 대한 평균값은 가중치 필터가 주변 픽셀 값을 이용해 새로운 픽셀을 생성하므로 서로 비슷했다. 하지만 히스토그램 분포가 조금 달랐는데, 노이즈가 많은 이미지는 노이즈로 인해 밝기 값이 넓은 범위에 걸쳐 분포되어 있어 표준 편차 값이 조금 더 크게 나왔다. 반면 스무딩된 이미지는 전반적으로 밝기 값이 균등하게 분포되어 있고, 표준 편차가 감소되어 있다.
Non-Linear Smoothing Spatial Filter

이번에는 비선형 스무딩 필터에 대해 알아보자. 선형 필터는 평균 필터와 같이 픽셀 값의 단순한 가중 평균을 사용하지만, 비선형 필터는 다른 접근 방식을 사용하여 이미지를 스무딩 한다. 즉, 전자는 이미지에 대해 고정된 연산을 적용(가산성, 동차성, 이동 불변성을 만족)하지만, 후자는 픽셀 값에 따라 다른 연산을 적용한다.
- 가산성(Additivity): 두 이미지에 필터를 적용한 결과를 합치면, 두 이미지를 합친 후 필터를 적용한 결과와 동일
- 동차성(Homogeneity): 이미지의 모든 픽셀 값을 스케일링하면, 필터를 적용한 결과도 동일한 스케일로 변함
- 이동 불변성(Shift Invariance): 이미지를 이동시켜도 필터를 적용한 결과의 패턴은 이동된 이미지와 동일하게 유지
I = imread("example2.jpg");
In = imnoise(I, 'salt & pepper');
비선형 필터에 대해 알아보기 위해, 각 픽셀의 값을 해당 픽셀 주변의 값들 중앙값으로 대체하는 중앙값(Median) 필터를 사용해 보자. 해당 필터는 소금-후추 노이즈(salt and pepepper noise)와 같은 극단적인 노이즈에 효과적이다.
Im(:,:,1) = medfilt2(In(:,:,1), [3 3]);
Im(:,:,2) = medfilt2(In(:,:,2), [3 3]);
Im(:,:,3) = medfilt2(In(:,:,3), [3 3]);
w = ones(3,3) ./ 9;
Ir = imfilter(In, w);
매트랩에서는 이미지에 중앙값 필터를 씌울 수 있는 medfilt2() 함수를 제공한다. 하지만 이 함수는 2차원 이미지까지만 적용이 가능하므로, RGB 3차원을 쓰는 컬러 영상에선 각 채널마다 medfilt2() 함수를 수행해줘야 한다. 이때 선형 필터와 비교를 위해 3x3 평균 가중치 필터를 씌운 이미지도 하나 생성했다.
figure(1);
subplot(1,3,1); imshow(Ir);
subplot(1,3,2); imshow(In);
subplot(1,3,3); imshow(Im);
왼쪽부터 평균 가중치 필터를 씌운 이미지, 노이즈 이미지, 중앙값 필터가 씌워진 이미지다. 확실히 선형 필터에서는 노이즈를 깔끔하게 지우지 못했지만, 비선형 필터에서는 소금-후추 노이즈를 제거하였다.
[cnt1, bin1] = imhist(Ir);
[cnt2, bin2] = imhist(In);
[cnt3, bin3] = imhist(Im);
fprintf("Ir: %d\n", max(cnt1));
fprintf("In: %d\n", max(cnt2));
fprintf("Im: %d\n", max(cnt3));
figure(2);
subplot(1,3,1); imhist(Ir);
subplot(1,3,2); imhist(In);
subplot(1,3,3); imhist(Im);
fprintf("I: %.2f\n", std(double(Ir(:))));
fprintf("In: %.2f\n", std(double(In(:))));
fprintf("Im: %.2f\n", std(double(Im(:))));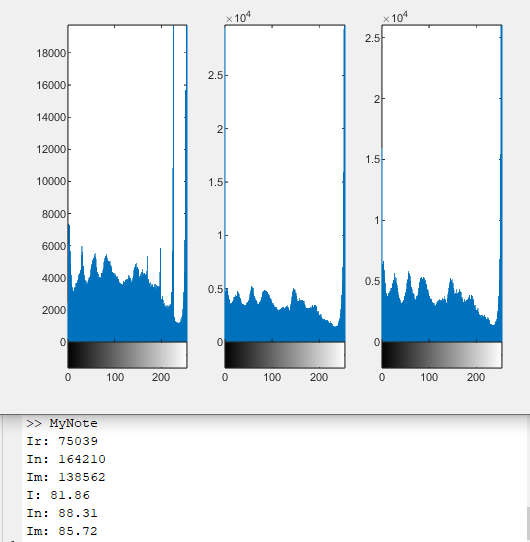
소금-후추 노이즈가 극단적인 노이즈를 생성하므로 픽셀 값의 최댓값과 최솟값의 변화가 있을 것이라 추측하고 다음과 같이 히스토그램을 비교해 보았다. 평균 가중치 필터는 이미지의 전반적인 밝기를 균등하게 분포하므로 최댓값이 중앙값 필터에 비해 상대적으로 절반만큼 줄었다. 이로 인해 표준 편차의 변화도 더 크게 나타났다.
요약
스무딩 공간 필터
1. 정의: 노이즈를 줄이고 블러링을 하는 필터
2. 특징
a. 이미지의 세부 사항을 줄이고, 그 공간을 주변 픽셀 값들을 이용해 채움
b. 이미지가 부드러워지는 대신, 화질이 떨어질 수 있음
3. 종류: 선형 필터, 비선형 필터
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Image Sharpening (2) (0) | 2023.11.07 |
|---|---|
| [디지털영상처리] Image Sharpening (1) (0) | 2023.11.06 |
| [디지털영상처리] Spatial Filtering (1) (2) | 2023.11.02 |
| [디지털영상처리] Histogram Processing (2) (0) | 2023.10.17 |
| [디지털영상처리] Histogram Processing (1) (2) | 2023.10.16 |