Data Clustering
개요

데이터 클러스터링(Data Clustering)은 비슷한 특성을 가진 데이터들을 같은 그룹으로 묶는 과정을 의미한다. 이를 통해 데이터를 분류하거나 단순화할 수 있으며, 레이블이 없는 데이터를 처리하므로 비지도 학습으로 분류된다. 클러스터링은 데이터의 이해를 돕고, 숨겨진 패턴을 발견하는 데 유용하게 사용된다.
데이터 클러스터링은 크게 Hard Clustering과 Soft Clustering으로 나뉜다. Hard Clustering은 각 데이터 포인트를 하나의 클러스터에 할당하는 방식이고, 대표적인 알고리즘으로 K-means Algorithm이 있다. 반면, Soft Clustering은 데이터 포인트를 여러 클러스터에 확률적으로 할당하는 방식으로, Expectation Maximization (EM)이 이 방법의 대표적인 알고리즘으로 알려져 있다. 이번 시간에는 이 두 알고리즘에 대해 알아보도록 하겠다.
본문
K-means Algorithm

K-means Clustering은 데이터를 k개의 클러스터로 분류하는 비지도 학습 알고리즘이다. 이 알고리즘은 사용자가 정의한 k값, 즉 클러스터의 개수를 기반으로 데이터를 그룹화한다. 해당 알고리즘은 각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작하는데, 해당 알고리즘의 과정은 다음과 같다.
- 초기화: 초깃값을 기준으로 k개의 클러스터 중심을 무작위로 선택
- 할당: 각 데이터 포인터들을 가장 가까운 클러스터 중심에 할당
- 업데이트: 현재 할당된 데이터 포인트의 평균으로 클러스터 중심을 업데이트
- 반복: 클러스터의 할당이 변하지 않거나, 지정된 반복 횟수에 도달할 때까지 2번과 3번의 과정을 반복
이 과정에서 초기 중심값을 선택하는 것이 결과에 큰 영향을 미친다. 따라서 초깃값을 잘못 잡게 되면 지역 최적화 문제가 발생하거나, 수렴 속도가 느려지는 등 다양한 문제가 발생할 수 있다. 이를 완화하기 위해 초기 클러스터 중심을 데이터 포인트 중에서 선택하거나, 알고리즘을 여러 번 실행하여 그 결과로 나온 클러스터링 중 가장 좋은 것을 선택하는 등의 다양한 전략이 존재한다.
중요한 점은, k-means 알고리즘이 항상 동일한 결과를 보장하지 않으며, 사용자가 거리 측정 방법(유클리디안(Euclidean) 거리, 코사인(Cosine) 거리 등)을 지정해야 한다는 것이다. 이는 데이터의 특성과 분석의 목적에 따라 결정되며, 다양한 시나리오와 문제에 맞게 적용하면 된다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data[:, :2]이제 k-means 클러스터링 알고리즘을 구현해 보자. 먼저 데이터 셋으로 iris를 불러와준다.
def k_means_clustering(data, k=3, n=100, tol=1e-4):
centers = data[np.random.choice(np.arange(len(data)), k, False)]
for _ in range(n):
labels = np.argmin(np.sqrt(((data - centers[:, np.newaxis])**2).sum(axis=2)), axis=0)
new_centers = np.array([data[labels == z].mean(axis=0) for z in range(k)])
if np.linalg.norm(new_centers - centers) < tol:
break
centers = new_centers
return centers, labelsk-mean clustering을 구현한 함수다. 클러스터링을 진행할 데이터 data, 클러스터 수 k, 최대 반복 횟수 n, 알고리즘 종료 기준값 tol을 인자로 받아온다. 그리고 데이터 포인트에서 무작위로 k개의 점을 선택하여 초기 클러스터의 중심 centers로 설정한다.
반복문을 순회하며 각 데이터 포인트에 대해, 모든 클러스터 중심과의 거리를 계산하고, 가장 가까운 클러스터의 인덱스 labels에 할당한다. 여기서 거리는 유클리디안 거리다. 그리고 현재 할당된 레이블을 기반으로 새로운 클러스터 중심을 계산하여 new_centers에 업데이트한다. 그 후 새로 계산한 클러스터 중심과 이전의 클러스터 중심의 변화량을 계산하여, 이 변화량이 tol보다 작다면 알고리즘을 종료한다.
centers, labels = k_means_clustering(data, 3)
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.title("K-Means Clustering: Iris Data (Sepal Length vs. Width)")
plt.show()
(centers, labels)
총합본
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data[:, :2]
def k_means_clustering(data, k=3, n=100, tol=1e-4):
centers = data[np.random.choice(np.arange(len(data)), k, False)]
for _ in range(n):
labels = np.argmin(np.sqrt(((data - centers[:, np.newaxis])**2).sum(axis=2)), axis=0)
new_centers = np.array([data[labels == z].mean(axis=0) for z in range(k)])
if np.linalg.norm(new_centers - centers) < tol:
break
centers = new_centers
return centers, labels
centers, labels = k_means_clustering(data, 3)
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.title("K-Means Clustering: Iris Data (Sepal Length vs. Width)")
plt.show()
(centers, labels)Expectation Maximization

기댓값 최대화(Expectation Maximization) 알고리즘은 각 클러스터가 특정 확률 분포를 가지고 있을 때, 데이터 포인트가 각 클러스터에 속할 확률을 최적화하는 데 사용되는 비지도 학습 기법이다. 이는 주로 데이터가 여러 확률 분포의 혼합으로 생성되었다고 가정할 때 사용되며, 각 클러스터는 특정 확률 분포를 나타낸다. 즉, 우리가 모델링하려는 데이터 세트 내에서 일부 데이터가 누락되었거나 관찰되지 않았을 때 EM 알고리즘은 이러한 누락된 데이터를 추정하고 모델 파라미터를 업데이트하는 데 사용된다.
일반적으로 최대 우도 추정치(Maximum Likelihood Estimate, MLE)를 찾는 데 사용되는 이 알고리즘은 관찰된 데이터 X와 누락된 데이터 또는 잠재 변수 Z를 이용해 우리가 추정하려는 모델의 파라미터에 대한 기댓값을 최대로 하게 한다. 여기서 θ는 모델이 데이터를 어떻게 설명하고 예측할 것인지를 결정하는 값들을 의미한다. 예를 들어, 선형 회귀 모델에서 y = ax + b라는 함수가 있다면, 해당 함수에서 θ는 a와 b다. 왜냐하면 이 두 값이 변하면 모델의 데이터를 설명하고 예측하는 방식이 변하기 때문이다. MLE는 모수가 미지의 θ인 확률 분포에서 추출한 데이터셋 X를 바탕으로 θ를 추정하는 기법이다.
이제 파라미터 θ를 찾아보자. θ를 찾기 위해 현재 파라미터 추정치 θ(t)에 대한 파라미터 θ의 함수를 정의하면 다음과 같다.
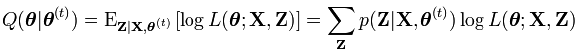
이러한 수식을 만족하는 Z의 조건부 기댓값을 찾는 것을 Expectation Step, E step이라고 한다. 만약 초기 추정치 θ가 없다면, k-means 클러스터링을 사용하여 초기 중심을 결정하거나, 랜덤 하게 초기 값을 선택한다. 그 후 해당 함수를 풀면 되는데, 수식이 굉장히 복잡하므로 궁금하다면 접은 글을 눌러 확인하면 된다.

Q 함수(Q-function)는 현재 파라미터 θ(t)의 하에서 다음 단계의 파라미터를 업데이트하는 기댓값 함수다.
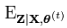
이 수식은 현재 파라미터 θ(t)와 관측 데이터 X에 대한 잠재 변수 Z의 조건부 기댓값을 나타낸다. 이때 Z는 잠재 변수(Latent Variable)로서, 우리가 직접적으로 관측할 수 없는 변수(누락된 데이터)를 의미한다. 우리의 목표는 누락된 데이터 Z를 추정하는 것인데, θ와 X를 이용해 어떻게 Z를 추정할 수 있는 것일까?
누락된 데이터는 직접적으로 관측할 수 없기 때문에, 이를 가능한 추론 하려고 시도한다. 그렇게 하는 방법 중 하나가 현재 가지고 있는 데이터 X와 모델 파라미터 θ를 기반으로 Z의 확률 분포를 추정하는 것이다. 이를 수식으로 나타내면 다음과 같다.
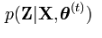
즉, 확률 분포는 X와 θ(t)가 주어졌을 때, 각 가능한 Z의 값이 얼마나 가능한지에 대한 정보를 제공한다. 그리고 E는 확률적으로 어떤 값이 나올 것인지를 기대하는 기댓값이므로, 확률 분포에 따른 가중치를 고려하여 평균을 취해야 하므로 다음과 같이 시그마를 씌운 형태로 바뀐다.

이제 우도 함수 log L(θ; X, Z)의 의미를 살펴보자. 일반적으로 우도 함수는 주어진 데이터 셋에 대해 다양한 파라미터 값들이 얼마나 그럴듯한 결과를 내는지 측정하는 함수다. 일반적으로 다음과 같은 수식을 사용한다.

여기서 X는 관측된 데이터, θ는 모델의 파라미터다. 이 함수는 파라미터가 주어졌을 때 데이터 X가 관측될 확률을 나타낸다. 일반적으로 로그 우도 함수를 사용하는데, 이는 계산을 더 간단하게 하고 수치적으로 더 안정적이기 때문이다.
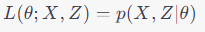
만약 데이터 X 외에도 잠재 변수 Z가 모델에 포함되어 있다면, 우도 함수는 다음과 같이 정의된다. 이 경우, 파라미터 θ가 주어졌을 때, 데이터 X와 잠재 변수 Z가 동시에 관측될 확률을 나타낸다. 따라서 해당 수식을 풀면

이 된다.

여기서 주어진 데이터 X와 현재 파라미터 추정치를 이용해 잠재 변수 Z가 특정 값을 가질 확률 p(Z|X, θ(t))에 베이지안 룰을 적용한다. 이는 데이터가 많고, 복잡한 상황에서 사후 확률을 계산하기 어려워 사전 확률과 우도를 사용하여 간접적으로 계산하기 때문이다.
E-Step을 통해 잠재 변수 Z의 조건부 확률 분포 p(Z|X, θ(t))를 계산했으면, Maximization, M-Step에서 파라미터 θ를 업데이트하면 된다. 이를 수식으로 나타내면 다음과 같다.

이렇게 업데이트된 θ값은 다음 라운드의 E-Step에서 사용되어, 다시 Q 함수를 업데이트하고, 이 과정이 수렴할 때까지 반복한다. 이때 로그 우도를 최대화하는 새로운 파라미터를 찾기 위해서 일반적으로 Q 함수를 θ에 대해 미분하고, 그 미분이 0이 되는 θ를 찾아 최대값을 찾는다. 그러나, 실제 계산은 모델의 세부 사항에 크게 의존한다는 점을 체크해두자.
요약
데이터 클러스터링
1. 정의: 비슷한 특성을 가진 데이터들을 같은 그룹으로 묶는 과정
2. 종류: Hard Clustering, Soft Clustering
K-means 클러스터링
1. 정의: 데이터를 k개의 클러스터로 분류하는 비지도 학습 알고리즘
2. 과정
a. 초기화: 초깃값을 기준으로 k개의 클러스터 선택
b. 할당: 거리를 이용해 클러스터 중심에 할당
c. 업데이트: 평균을 이용해 클러스터 중심 업데이트
d. 반복
3. 특징: 거리를 사용자가 알맞게 정의해야 하며, 초깃값에 따라 결과가 바뀔 수 있음
EM 알고리즘
1. 정의: E-Step과 M-Step을 이용해 각 클러스터가 속할 확률을 계산하는 비지도 학습 알고리즘
2. 과정
a. E-Step: 조건부 확률 p(Z|X,θ(t)) 값 계산
b. M-Step: θ(t) 업데이트
3. 특징: 누락된 데이터를 추정하고, 모델 파라미터를 업데이트할 때 사용
'CS > 딥러닝' 카테고리의 다른 글
| [딥러닝] 선형 판별 분석(LDA) (2) | 2023.10.04 |
|---|---|
| [딥러닝] 주성분 분석(PCA) (2) | 2023.09.30 |
| [딥러닝] 비선형 회귀 분석(2) (0) | 2023.09.26 |
| [딥러닝] 비선형 회귀 분석(1) (1) | 2023.09.25 |
| [딥러닝] 머신러닝과 1차 선형 회귀 (0) | 2023.09.11 |