Linear Discriminant Analysis
개요

선형 판별 분석(Linear Discriminant Analysis, LDA)은 데이터를 차원 축소하고 분류하는 지도 학습 기법 중 하나다. LDA는 PCA와 유사한 점을 가지고 있지만, 클래스 레이블 정보를 활용하며, 분류 목적에 최적화된 축을 찾는 데 중점을 둔다. 이번 시간에선 LDA의 원리와 적용 방법에 대해 다루어보겠다.
본문
Supervised Learning
지도 학습(Supervised Learning) 은 입력 데이터와 그에 상응하는 정답 레이블을 사용하여 모델을 학습시키는 방식을 의미한다. 이러한 방식은 모델이 입력 데이터와 출력 레이블 간의 패턴을 학습하게 해, 미래의 유사한 데이터에 대한 출력을 예측하도록 한다. LDA는 주어진 입력과 관련된 클래스(출력 y)를 예측하기 위해 사용되므로, 이것을 지도 학습의 한 형태로 볼 수 있다.
LDA의 주요 목표
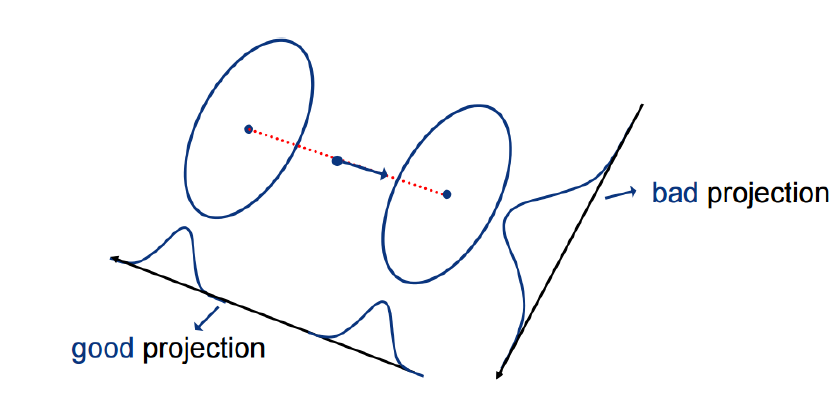
LDA는 데이터의 클래스 레이블을 최대한 유지하면서 차원을 축소하고, 클래스 간의 거리를 최대화하고, 클래스 내의 분산을 최소화하는 방향으로 데이터를 투영한다. 위의 사진에서 bad projection 방향으로 투영하면 데이터가 분류가 되지 않아 나쁜 투영이 되고, good projection 방향으로 투영하면 데이터가 잘 분류되어 좋은 분류가 된다.
LDA 과정 및 구현
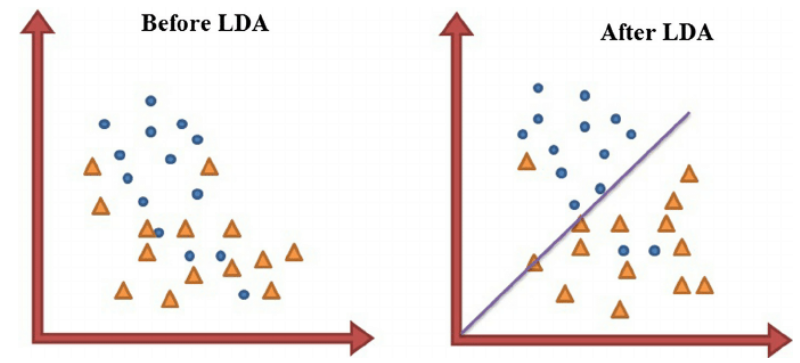
LDA도 PCA와 마찬가지로 최적의 기저 개념이 존재한다. 다만 여기서 최적의 기저란 클래스 간 분산을 최대화하고 클래스 내 분산을 최소화하는 축을 의미한다. LDA에서도 최적의 기저는 미리 정해진 것이 아니라, 클래스를 가장 잘 구분하는 방향을 찾는 과정을 통해 결정된다.
- 각 클래스의 평균을 계산
- 클래스 내 분산을 계산하고, 두 클래스의 산포를 합침
- 클래스 간 분산을 구하기 위해 두 클래스의 평균 간의 차이를 계산
- 두 클래스의 분산을 합친 행렬의 역행렬과 클래스 간 분산을 최적화 문제로 풀어서, 데이터를 투영할 최적의 벡터 계산
- 찾아낸 벡터를 사용하여 데이터를 새로운 축에 투영
- 분류 규칙을 정의한 후 새로운 데이터로 분류
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
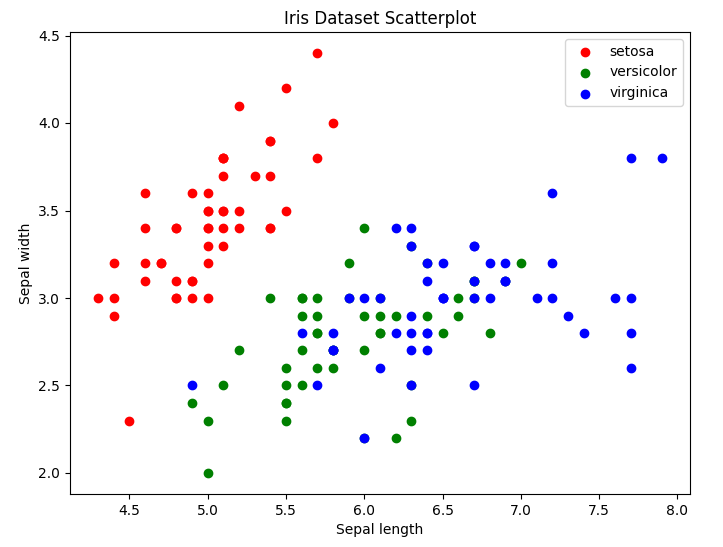
target_names = iris.target_names위와 같이 setosa, versicolor, virginica 3개의 클래스가 길이와 높이로 구분되어 있다고 가정해 보자. iris 데이터를 불러와 X값과 y값에 iris의 데이터와 타깃을 초기화한다.
means = []
for class_label in np.unique(y):
means.append(np.mean(X[y == class_label], axis=0))
overall_mean = np.mean(X, axis=0)각 클래스별 평균을 계산하기 위해 빈 리스트인 means에 모든 클래스 레이블에 대해 평균을 계산한다. 여기서 X[y -== class_label]은 boolean 인덱싱을 사용하여 특정 클래스에 속하는 모든 샘플을 선택하고, 선택된 샘플에 대해 피처별 평균을 계산한다. 그 결과를 리스트에 추가한다. 그리고 전체 데이터셋 평균을 overall_mean에 할당하였다.
S_W = np.zeros((X.shape[1], X.shape[1]))
for class_label, mean_vector in zip(np.unique(y), means):
class_sc_mat = np.zeros((X.shape[1], X.shape[1]))
for row in X[y == class_label]:
row, mv = row.reshape(X.shape[1], 1), mean_vector.reshape(X.shape[1], 1)
class_sc_mat += (row - mv).dot((row - mv).T)
S_W += class_sc_mat클래스 내 산포 행렬을 계산하기 위해 S_w를 모든 요소가 0인 행렬로 시작하여, 각 클래스에 대한 산포를 누적하게 하였다. 모든 클래스에 대해 각 샘플의 산포를 개별적으로 계산하고, 이를 클래스 별로 누적하고, 마지막으로 이를 전체 행렬에 누적하는 코드다.
S_B = np.zeros((X.shape[1], X.shape[1]))
overall_mean = overall_mean.reshape(X.shape[1], 1)
for mean_vector in means:
n = X[y == class_label].shape[0]
mv = mean_vector.reshape(X.shape[1], 1)
S_B += n * (mv - overall_mean).dot((mv - overall_mean).T)클래스 간 산포 행렬을 계산하기 위해 S_B를 모든 요소가 0인 행렬로 시작하여, 각 클래스의 평균과 전체 데이터의 평균 간의 차이를 바탕으로 클래스 간 분산을 측정하였다. 이때 전체 데이터의 평균 벡터도 열 벡터로 재구성하였다.
eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)그리고 최적화를 계산하기 위해 Sw와 SB를 이용하여 고유값과 고유벡터를 계산한다. 즉, 클래스 내 산포 행렬의 역행렬과 클래스 간 산포 행렬의 곱을 계산하고, 고윳값의 절댓값과 해당 고유벡터로 형성한 튜플을 생성하였다. 마지막으로 리스트를 고윳값의 크기에 따라 내림차순으로 정렬하였다.
W = np.hstack([eig_pairs[i][1].reshape(X.shape[1], 1) for i in range(len(target_names) - 1)])
X_lda = X.dot(W)가장 큰 고유값을 가진 k개의 고유벡터를 선택하고, 데이터를 새로운 공간으로 투영하였다.
plt.figure(figsize=(8, 6))
colors = ['r', 'g', 'b']
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], alpha=.8, color=color, label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of IRIS dataset')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.grid()
plt.tight_layout()
plt.show()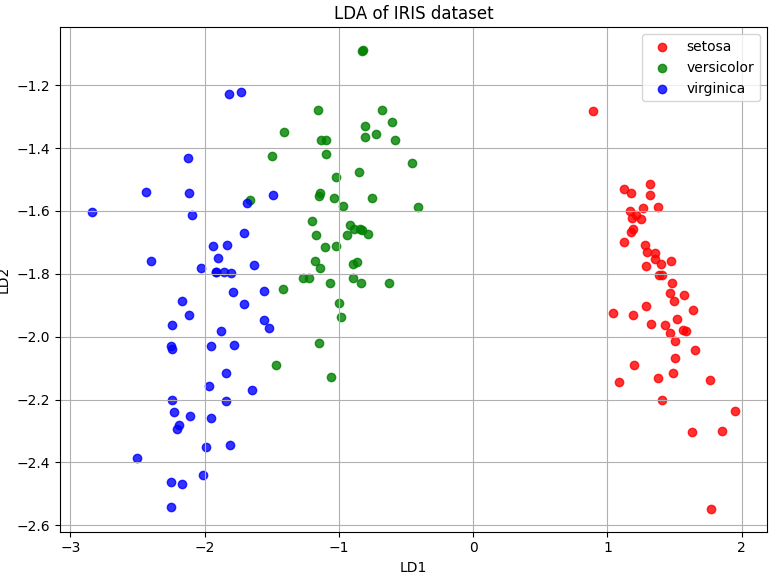
마지막으로 그래프를 띄우는 코드를 추가하였다.
라이브러리를 활용한 코드
위의 코드는 과정을 자세히 다루기 위해, 관련 라이브러리를 다루지 않아 코드가 길어졌다. 이번엔 scikit-learn에서 제공하는 LDA 클래스를 사용하면 LDA를 쉽게 적용해 볼 수 있다. 아래의 코드는 iris 데이터셋에 LDA를 적용하고, 결과를 2차원 공간에 시각화하는 예제다.
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
lda = LinearDiscriminantAnalysis(n_components=2) # number of components to keep
X_r2 = lda.fit(X_train, y_train).transform(X_train)
plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_r2[y_train == i, 0], X_r2[y_train == i, 1], color=color, alpha=.8,
label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of IRIS dataset')
plt.show()
요약
LDA
1. 정의: 데이터의 차원을 줄이고, 클래스를 이용하여 데이터를 분류하는 방법
2. 특징
a. 지도 학습
b. 클래스 내 분산은 최소화, 클래스 간 분산은 최대화
3. 과정
- 평균 계산 → 클래스 내/외 산포 행렬 계산 → 고유값, 고유벡터 계산 → 새로운 축에 투영
'CS > 딥러닝' 카테고리의 다른 글
| [딥러닝] Data Clustering (0) | 2023.10.09 |
|---|---|
| [딥러닝] 주성분 분석(PCA) (2) | 2023.09.30 |
| [딥러닝] 비선형 회귀 분석(2) (0) | 2023.09.26 |
| [딥러닝] 비선형 회귀 분석(1) (1) | 2023.09.25 |
| [딥러닝] 머신러닝과 1차 선형 회귀 (0) | 2023.09.11 |