머신러닝 개요
개요
인공지능(Artificial Intelligence)은 인공적인 방법을 통해 인간의 지능을 모방하는 컴퓨터과학의 분야 중 하나다. 이는 합리적인 추론을 통해 문제를 해결하거나, 기계가 세상에 대한 지식을 표현하거나, 경로를 추적하거나, 데이터를 학습하여 입력과 출력 사이의 함수를 찾는 등 다양한 분야에서 응용되고 있다. 즉, 기계가 인간처럼 사고하고 학습하며 작업을 수행하는 능력을 가진 것을 인공지능이라고 한다.
이러한 인공지능은 매우 넓은 분야로서, 여러 하위 분야를 포함하고 있다. 주요 분야로는 머신러닝(Machine Learning), 로보틱스(Robotics), 전문가 시스템(Expert Systems), 자연어 처리(Natural Language Processing), 컴퓨터 비전(Computer Vision) 등이 있다.
이중 머신러닝은 데이터를 바탕으로 알고리즘을 학습시키는 인공지능 학문이다. 머신러닝은 크게 3가지로 학습 방법론을 나눌 수 있는데, 먼저 관측된 입력-출력 쌍의 데이터로부터 모델을 학습시키는 지도학습(Supervised Learning)이 있다. 이 방식은 이미 알려진 답이 있는 데이터를 사용하여 알고리즘을 훈련시킨 후, 새로운 데이터에 대한 예측을 수행한다. 반대로 비지도 학습(Unsupervised Learning)은 레이블이 없는 데이터를 사용하여 알고리즘을 학습시킨다. 즉, 데이터의 숨겨진 패턴이나 구조를 찾는데 주로 사용된다. 이 외에도 사용자가 환경과 상호작용하며 보상을 최대화하는 행동을 학습하는 강화학습(Reinforcement Learning)이 있다.
이번 시간에는 인공지능의 분야 중 하나인 머신러닝의 지도학습 방법 중 하나, 선형 회귀(Linear Regression)에 대해 알아보도록 하자.
본문
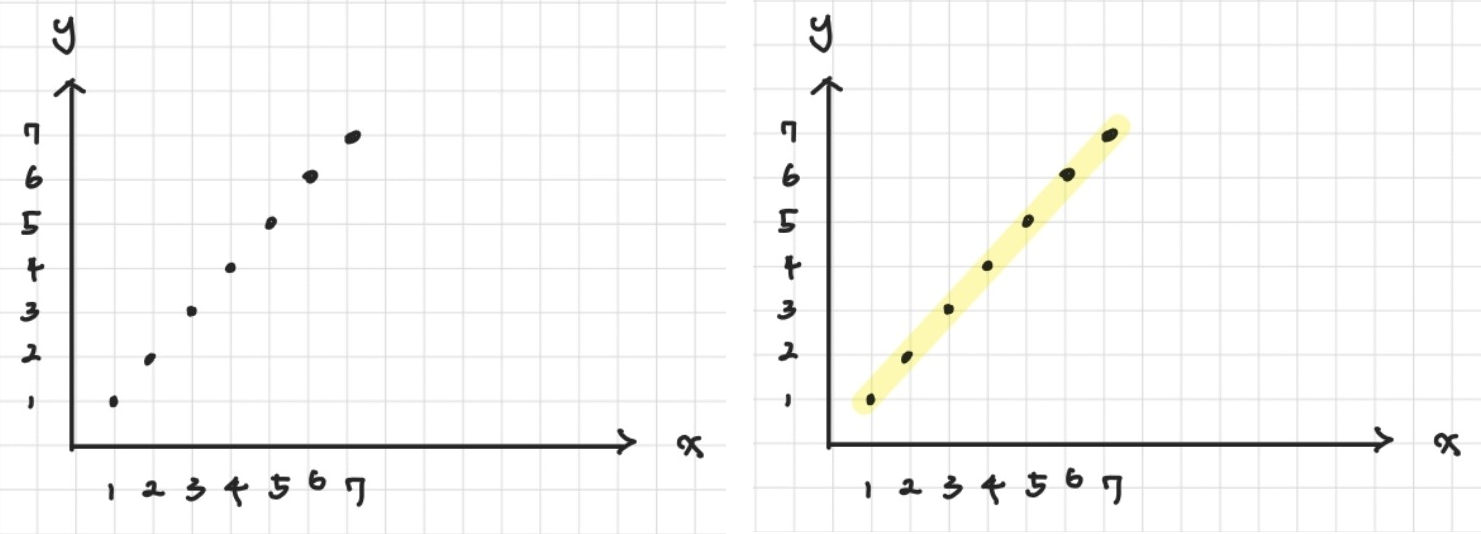
다음과 같은 데이터쌍 (1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (7,7)이 그래프 상에 표현되어 있다고 해보자. 이때 x와 y 사이의 관계는 관측되는 좌표 평면에 의해 y = x로 표현할 수 있다. 이처럼 알려진 데이터를 가장 잘 설명하게 두 데이터 사이의 관계를 모델링하는 것을 회귀(Regression)라고 한다. 회귀를 통해 얻은 모델은 새로운 독립 변수 값에 대한 종속 변수 값을 예측하는 데 사용될 수 있다. 이러한 회귀는 모델을 선형적으로 표현할 수 있다고 가정하고 분석을 진행하는 선형 회귀(Linear Regression), 다항 회귀(Polynomial Regression), 비선형 회귀(Non-linear Regression)로 나뉜다.
선형 회귀(Linear Regression)

하지만 실제로 데이터를 분석할 때, 모든 데이터가 완벽하게 회귀선에 위치하는 상황은 드물다. 이는 관측던 데이터 중 일반적인 분포를 벗어나는 이상치(Outlier)의 존재 때문이다. 이상치는 다양한 원인으로 발생할 수 있는데, 데이터 수집 과정의 오류나, 데이터 입력 시의 실수로 인한 잘못된 값 입력 등이 그 원인 중 일부다. 이런 이상치 하나만으로도 함수의 기울기와 절편이 크게 변할 수 있어, 데이터의 정확성과 모델의 예측 능력에 큰 영향을 미칠 수 있다.
그렇다면 어떻게 이러한 오차를 줄여 데이터를 예측하는 회귀를 진행할 수 있을까? 오차를 최소화하기 위해 예측한 출력과 실제 출력의 차이인 손실 함수(Loss Function)를 이용하면 이를 해결할 수 있다. 위의 그래프에서 이상치 점과 직선 사이에 수선의 발을 내리면 손실값(Loss)을 얻을 수 있는데, 이들의 누적합을 제곱 오차(Squared Error)라고도 부른다.
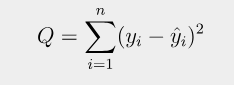
즉, 이 제곱 오차들의 합을 최소화하는 것이 선형 회귀를 최적화하는 방법 중 하나라고 할 수 있다. 이를 위해 해당 식을 조금 변형하면 다음과 같이 나타낼 수 있다. 이때 제곱을 하는 이유는 오차의 값을 양수로 두고, 편차가 큰 것을 더욱 부각하기 위한 것이다.
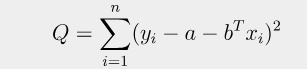
여기서 모델의 예측값을 해당 꼴로 바꿀 수 있는 이유는, 모델의 예측값이 입력 변수들과 그에 해당하는 가중치들의 선형 조합으로 구성되기 때문이다. 이로 인해 Q를 최소화하는 것이 a와 b를 찾는 문제로 바뀌었다.
경사 하강법(Gradient Descent Method)
주어진 식을 최소화하는 a와 b를 찾으려면, 손실 함수를 a와 b에 대해 각각 미분하면 해를 구할 수 있다. 이러한 방식으로 문제에 대한 해답을 명확하게 제시하는 closed-form solution을 구해야 하는데, 이는 함수의 차원이 높아질수록 불가능해진다. 따라서 수치해석적으로 점차 정답에 가깝게 다가가는 것을 경사 하강법이라고 한다.
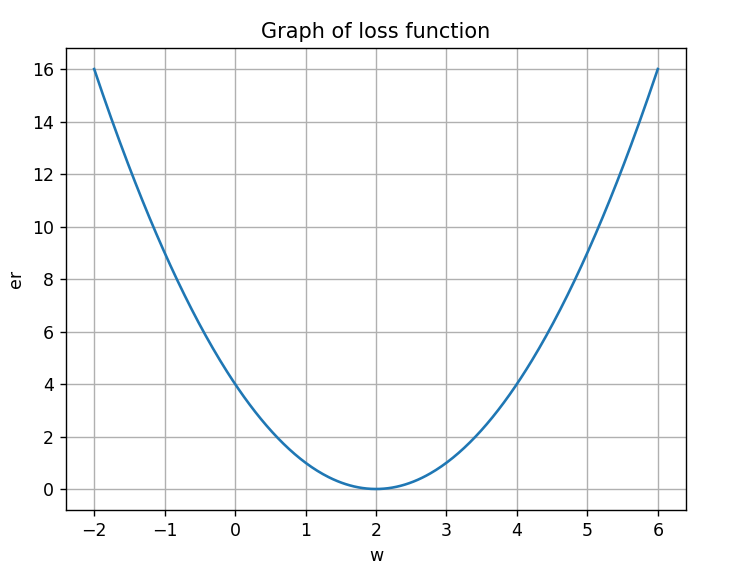
경사 하강법의 기본 원리는 임의의 점에서 시작하여 에러의 기울기의 반대 방향으로 이동하는 것이다. 예를 들어 위와 같이 y = (x-2)^2 함수가 존재한다고 해보자. 우리의 목표는 임의의 점 w0로부터 시작하여 Gradient가 0이 되는 곳을 찾는 것이다.

위 그래프에서 빨간색 점들은 경사 하강법을 사용하여 w값을 업데이트하는 과정을 나타낸다. 즉, 임의의 점 w = 0에서 시작하여 기울기가 감소하는 +w의 방향으로 점들을 이동시키며 w = 2에 근접하게 하는 방법이 경사 하강법이다. 이를 수식으로 표현하면 다음과 같다. 이때 전체 데이터 배치(데이터를 일정한 크기의 그룹으로 나눈 것)를 사용하여 경사를 업데이트하여 배치 경사 하강법(Batch Gradient Descent)라고도 부른다.

확률적 경사 하강법(Stochastic Gradient Descent Method)

앞서 설명한 경사 하강법은, 전체 데이터를 사용하여 기울기를 업데이트하기 때문에 지역 최솟값(Local Minimum) 문제가 발생할 수 있다. 위의 그래프에서 파란색 선은 (w-2)(w+2)(w-4) 함수를 나타낸다. 이 함수는 여러 개의 굴곡을 갖고 있기 때문에, 경사 하강법을 사용할 때 시작 위치에 따라 전역 최솟값(Global minimum)이 아닌 지역적인 최솟값에 도달할 수 있다. 즉, 초깃값을 w = 1로 시작했을 때, 경사 하강법은 w의 값이 약 3에 수렴하게 되어 전역 최솟값에 도달하지 못하고 지역 최솟값에 갇힌다.
또한 전체 데이터를 한 번에 메모리에 올리기 때문에 메모리 문제도 발생한다. 따라서 이를 해결하기 위해 전체 데이터셋에서 임의의 한 개의 데이터 포인트를 무작위로 선택해 그 포인트에 대한 기울기를 계산하는 확률적 경사 하강법을 사용하면 해결할 수 있다.

물론 해당 방법 또한 지역 최솟값 문제에 빠질 수는 있지만, 기존의 경사 하강법보다 더욱 뛰어난 성능을 보인다는 점에서 의의를 갖고 있다. 즉, 로컬 미니멈의 확률을 낮추고, 메모리를 모두 쓰지 않아 효율적이다.
코드 예제
Batch Gradient Descent Method
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
def gradient_descent(a, b, n):
# Define symbolic variable and function
w_symbol = sp.symbols("w")
func_symbol = (a * w_symbol - b) ** n
# Create a numpy function for plotting and evaluation
func_numpy = sp.lambdify(w_symbol, func_symbol, "numpy")
start_range = float(input("Enter the start of the range: "))
end_range = float(input("Enter the end of the range: "))
w_values_np = np.linspace(start_range, end_range, 400)
func_values_np = func_numpy(w_values_np)
# Plot the function
plt.figure(figsize = (10, 6))
plt.plot(w_values_np, func_values_np, label = f"Function: $({a}w-{b})^{n}$")
plt.xlabel("w")
plt.ylabel("y")
plt.title(f"Gradient Descent on $({a}w-{b})^{n}$")
plt.grid(True)
# Gradient Descent
learning_rate = 0.01
w_start = 0
w_trace = [w_start]
threshold = 0.001
iterations = 100
for _ in range(iterations):
gradient_value = sp.diff(func_symbol, w_symbol).subs(w_symbol, w_start)
w_start -= learning_rate * gradient_value
w_trace.append(w_start)
# Plot the points on the graph
func_trace = [func_numpy(w_val) for w_val in w_trace]
plt.scatter(w_trace, func_trace, c='red', marker='o', label='Gradient Descent Steps')
plt.legend()
plt.show()
return w_start
if __name__ == "__main__":
a = float(input("Enter the value of a: "))
b = float(input("Enter the value of b: "))
n = int(input("Enter the value of n: "))
result = gradient_descent(a, b, n)
print(f"Estimated minimum at w = {result:.4f}")해당 코드는 (aw-b)^n의 꼴의 함수에서 a와 b, n의 값을 입력했을 때 주어진 범위에서 경사 하강법을 적용하는 코드다.
Stochastic Gradient Descent Method
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
def gradient_descent(a, b, n):
# Define symbolic variable and function
w_symbol = sp.symbols("w")
func_symbol = (a * w_symbol - b) ** n
# Create a numpy function for plotting and evaluation
func_numpy = sp.lambdify(w_symbol, func_symbol, "numpy")
start_range = float(input("Enter the start of the range: "))
end_range = float(input("Enter the end of the range: "))
w_values_np = np.linspace(start_range, end_range, 400)
func_values_np = func_numpy(w_values_np)
# Plot the function
plt.figure(figsize = (10, 6))
plt.plot(w_values_np, func_values_np, label = f"Function: $({a}w-{b})^{n}$")
plt.xlabel("w")
plt.ylabel("y")
plt.title(f"Stochastic Gradient Descent on $({a}w-{b})^{n}$")
plt.grid(True)
# Stochastic Gradient Descent
learning_rate = 0.01
w_start = 0
w_trace = [w_start]
threshold = 0.001
iterations = 100
for _ in range(iterations):
random_index = np.random.randint(len(w_values_np))
w_random = w_values_np[random_index]
gradient_value = sp.diff(func_symbol, w_symbol).subs(w_symbol, w_random)
w_start -= learning_rate * gradient_value
w_trace.append(w_start)
# Plot the points on the graph
func_trace = [func_numpy(w_val) for w_val in w_trace]
plt.scatter(w_trace, func_trace, c='red', marker='o', label='SGD Steps')
plt.legend()
plt.show()
return w_start
if __name__ == "__main__":
a = float(input("Enter the value of a: "))
b = float(input("Enter the value of b: "))
n = int(input("Enter the value of n: "))
result = gradient_descent(a, b, n)
print(f"Estimated minimum at w = {result:.4f}")해당 코드는 (aw-b)^n의 꼴의 함수에서 a와 b, n의 값을 입력했을 때 주어진 범위에서 확률적 경사 하강법을 적용하는 코드다.
요약
인공지능
1. 정의: 인공적인 방법을 통해 인간의 지능을 모방하는 컴퓨터과학의 분야
2. 분야
- 머신러닝, 로보틱스, 전문가 시스템, 자연어 처리, 컴퓨터 비전
머신러닝
1. 정의: 데이터를 바탕으로 알고리즘을 학습시키는 인공지능 학문
2. 종류
- 지도 학습, 비지도 학습, 강화 학습
선형 회귀
1. 정의: 알려진 데이터를 가장 잘 설명하게 두 데이터 사이의 관계를 선형적으로 모델링하는 것
2. 경사 하강법
a. 정의: 수치해석적으로 점차 정답에 가깝게 다가가는 것
b. 종류: 배치 경사 하강법, 확률적 경사 하강법
'CS > 딥러닝' 카테고리의 다른 글
| [딥러닝] Data Clustering (0) | 2023.10.09 |
|---|---|
| [딥러닝] 선형 판별 분석(LDA) (2) | 2023.10.04 |
| [딥러닝] 주성분 분석(PCA) (2) | 2023.09.30 |
| [딥러닝] 비선형 회귀 분석(2) (0) | 2023.09.26 |
| [딥러닝] 비선형 회귀 분석(1) (1) | 2023.09.25 |