Principle Component Analysis(PCA)
개요
남자와 여자에 대한 다양한 특징 정보가 주어졌다고 가정해 보자. 이들을 구분하기 위한 정보는 굉장히 많을 것이다. 하지만 실질적으로 우리가 성별을 구분하기 위해서 이 모든 데이터를 활용할 필요가 없다. 예를 들면, 염색체만 확인하면 생물학적으로 남녀를 구분할 수 있다.
이러한 핵심 특징을 추출한다는 아이디어에 기반하여 AI 학습 전에 학습 데이터를 전처리하면 효과적인 머신 러닝을 진행할 수 있다. 여기서 말하는 전처리는 데이터의 차원을 줄이는 것을 의미하는데, 이를 Principle Component Analysis(PCA), 주성분 분석이라고 한다.
본문
비지도학습
PCA는 비지도 학습에 속한다. 비지도 학습(Unsupervised learning)은 레이블이나 목표 변수가 없는 학습 데이터만을 사용하여 데이터의 구조나 패턴을 찾는 학습 방법이다. 이러한 비지도 학습은 주로 클러스터링(Clustering)이나 차원 축소 등에 사용된다.
차원 축소
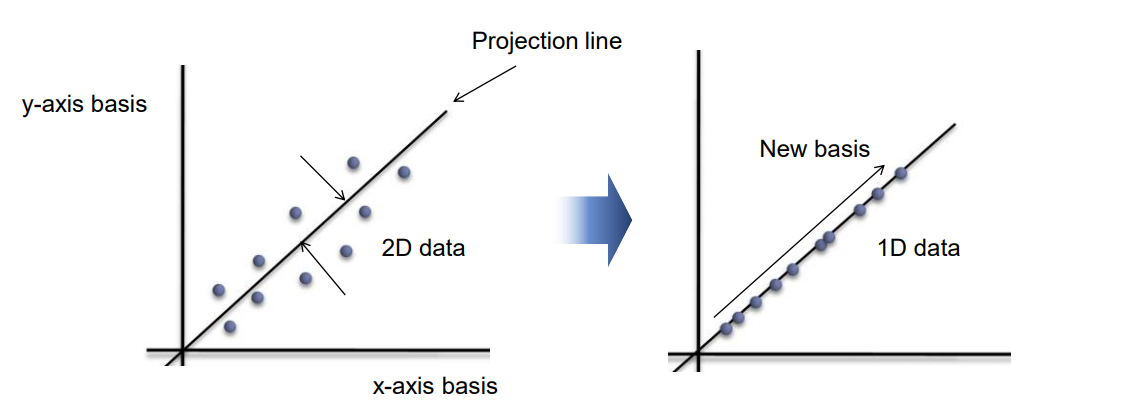
차원 축소(Dimensionality Reduction)는 데이터의 차원(특성의 수)을 줄이며 데이터의 중요한 정보를 최대한 보존하는 것을 의미한다. 일반적으로 데이터 추출 시, 노이즈 때문에 함수의 차원이 높아지고 비선형성이 커지는 경우가 많다. 이런 상황에서 차원 축소의 장점은 다음과 같다.
- 계산 효율성 증가: 데이터의 차원이 감소하면, 모델 학습과 예측에 필요한 계산량이 줄어듦
- 데이터 시각화: 차원을 축소함으로써, 데이터를 시각적으로 이해하는 것이 쉬워짐
- 노이즈 제거: 노이즈와 불필요한 정보를 제거
- 과적합 방지: 차원의 저주 문제를 해결하여 모델의 과적합을 줄임
- 차원의 저주(Curse of dimensionality)란 데이터 과학과 머신 러닝에서 데이터의 차원의 증가할수록 해당 공간의 크기가 기하급수적으로 증가하며, 데이터 분석이나 모델 학습에 어려움을 초래하는 현상을 의미한다.
반면, 차원 축소 시 데이터의 일부 정보 손실이 발생할 수 있으며, 어떤 차원을 유지하고 제거할지 결정하는 것이 복잡할 수 있다. 정보 손실로 인해 모델은 데이터의 복잡성을 충분히 표현하지 못해, 이는 under-fitting의 원인이 될 수 있다.
PCA의 주요 목표
PCA는 데이터의 주요 패턴을 캡처하면서 차원을 줄이는 분석 기법이다. 핵심 원리는 데이터의 분산을 최대화하는 주성분을 찾는 것이다. 분산은 데이터가 얼마나 특정 방향으로 퍼져 있는지를 나타내며, 큰 분산은 해당 방향에 데이터의 주요 정보나 패턴이 포함되어 있음을 의미한다. 따라서, 분산이 큰 주성분 방향으로 데이터를 투영함으로써 차원을 줄이면, 정보의 손실을 최소화할 수 있고 데이터들 사이의 차이점이 명확해진다.
PCA 과정

PCA를 수행할 때는 데이터의 구조를 가장 잘 반영하는 기저를 찾는 것이 중요하다. 이를 최적의 기저(Optimal Bases)라고 부르며, PCA에서는 자동으로 분산이 최대가 되는 방향, 즉 데이터 간의 중복성이 가장 적은 방향을 최적의 기저로 찾아낸다. 만약 중복성이 높은 기저를 선택하면, 비슷한 정보를 중복하여 포함하게 되므로, PCA의 주 목적인 정보 압축과 패턴 추출에 방해가 된다.
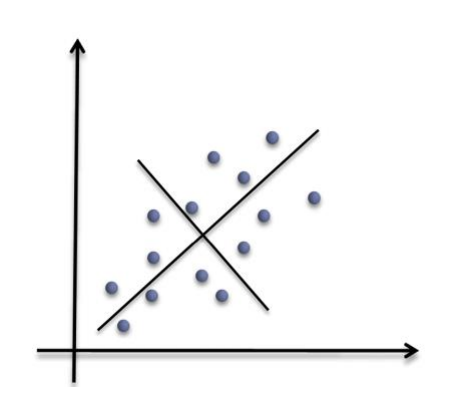
이때 기저들은 서로 수직이어야 한다.
- 평균 계산
- 데이터 중심화(Centering): 각 데이터에서 평균을 빼서 중심으로 데이터를 모음. 이는 센터링을 하지 않았을 때, 주성분 방향이 일치하지 않아 데이터의 분포가 이상해지기 때문
- 공분산(Covariance) 행렬 계산
- 고유값과 고유벡터 계산: 공분산 행렬에 decomposition을 적용해 고유값(Eigenvalue)과 고유벡터(Eigenvector)를 구함
- 주성분 선택: 가장 큰 고유값을 갖는 고유벡터로부터 원하는 수의 주성분을 선택

줄일 차원의 개수는 전체 고유값의 합에 대해 k번째 고유값이 차지하는 비율을 기반으로 누적된 분산이 전체 분산의 p%를 설명할 때까지의 고유벡터를 고른다. 이를 테면 90%로 설정하였으면, 해당 그래프에서 7~8개의 차원을 선택하는 것이고, 70%로 설정했으면 3개의 차원을 선택하는 것이 된다.
구현

import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
# 데이터 로딩
iris = load_iris()
# 원본 데이터를 데이터프레임으로 변환
df_original = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df_original['target'] = iris.target다음과 같이 iris 데이터의 차원을 줄여, 데이터를 분류해 보자. 데이터를 효율적으로 조작하고 분석하기 위해 원본 데이터를 데이터프레임 형태로 변환하였다. 이때 이 작업이 필요한 이유는, 데이터를 열과 행의 형태로 구조화하여 조작하기 위함이다.
# PCA 변환
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(df_original.iloc[:, :-1])
df_pca = pd.DataFrame(data=principalComponents, columns=['First Principal Component', 'Second Principal Component'])
df_pca['target'] = iris.target데이터를 2차원으로 줄이기 위해 PCA를 사용하였다. 이때 주성분을 추출하기 위해 pca.fit_transform() 함수를 사용하였다. 이를 적용하면 fit에서 찾은 주성분 방향으로 데이터를 투영하여 주성분 점수를 반환한다. 즉, target 열을 제외한 df_original의 데이터를 PCA로 변환하여 주성분 점수를 반환하게 하였다.
mean = df_original[['sepal length (cm)', 'sepal width (cm)']].mean().values
# 주성분 (고유벡터) 가져오기
w1 = pca.components_[0]
w2 = pca.components_[1]원본 데이터의 주성분 방향을 확인하기 위해 PCA의 고유 벡터를 w1과 w2에 할당하였다.

# 그래프 그리기
plt.figure(figsize=(18, 6))
# 원본 데이터 시각화
plt.subplot(1, 3, 1)
sns.scatterplot(data=df_original, x='sepal length (cm)', y='sepal width (cm)', hue='target', palette='viridis', legend='full')
plt.title("Original Data: Sepal Length vs Sepal Width")
# 원본 데이터에 화살표 추가하여 시각화
plt.subplot(1, 3, 2)
sns.scatterplot(data=df_original, x='sepal length (cm)', y='sepal width (cm)', hue='target', palette='viridis', legend='full')
plt.title("Original Data with Principal Component Directions")
plt.arrow(mean[0], mean[1], w1[0] * 0.3, w1[1] * 0.3, head_width=0.2, head_length=0.2, fc='red', ec='red')
plt.arrow(mean[0], mean[1], w2[0] * 0.3, w2[1] * 0.3, head_width=0.2, head_length=0.2, fc='blue', ec='blue')
plt.text(mean[0] + w1[0] * 0.15, mean[1] + w1[1] * 0.15, 'w1', color='red', fontsize=12, ha="center", va="center")
plt.text(mean[0] + w2[0] * 0.15, mean[1] + w2[1] * 0.15, 'w2', color='blue', fontsize=12, ha="center", va="center")
# PCA 데이터 시각화
plt.subplot(1, 3, 3)
sns.scatterplot(data=df_pca, x='First Principal Component', y='Second Principal Component', hue='target', palette='viridis', legend='full')
plt.title("PCA Data: First vs Second Principal Component")
plt.tight_layout()
plt.show()마지막으로 데이터가 어떻게 분포되었는지 확인하기 위해 다음 코드를 작성하면 위와 같은 그래프가 나온다.
요약
PCA
1. 정의: 분산이 최대화되는 방향으로 데이터를 줄임으로써, 데이터의 주요 패턴을 캡처하며 차원을 줄이는 기법
2. 특징
a. 비지도 학습
b. 차원 축소
- 정의: 데이터의 차원을 줄이는 것.
- 목표: 데이터의 정보 손실을 최소화
- 장점: 계산 효율성 증가, 데이터 시각화, 노이즈 제거, 과적합 해결
- 단점: 정보가 손실되며 under-fitting이 발생할 수 있음
3. 과정
- 평균 계산 → 데이터 중심화 → 공분산 행렬 계산 → 고유값, 고유벡터 추출 → 주성분 선택
'CS > 딥러닝' 카테고리의 다른 글
| [딥러닝] Data Clustering (0) | 2023.10.09 |
|---|---|
| [딥러닝] 선형 판별 분석(LDA) (2) | 2023.10.04 |
| [딥러닝] 비선형 회귀 분석(2) (0) | 2023.09.26 |
| [딥러닝] 비선형 회귀 분석(1) (1) | 2023.09.25 |
| [딥러닝] 머신러닝과 1차 선형 회귀 (0) | 2023.09.11 |