개발일지

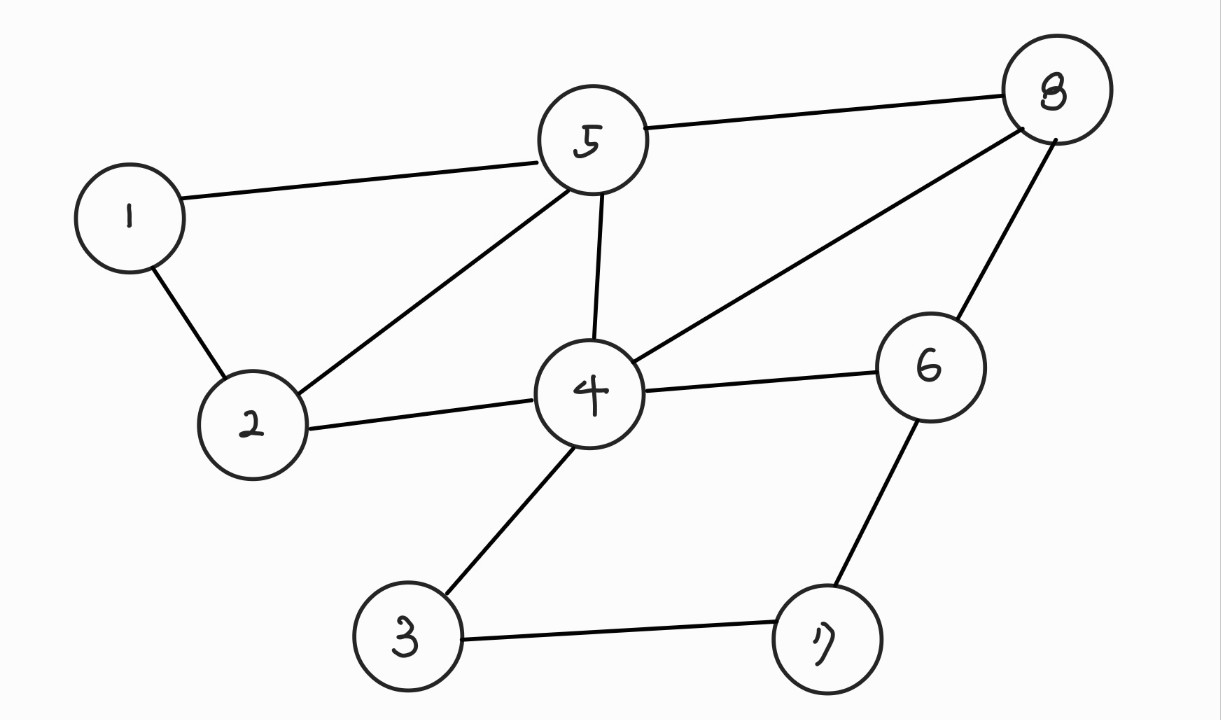
문제 설명 제한 사항 및 입출력 예제 개념 이 문제는 자연수 n을 연속한 자연수들의 합으로 표현하는 방법의 수를 찾는 문제다. n이 주어지면, 한 개 이상의 연속된 자연수의 합으로 n을 표현하는 방법의 수를 찾아야 한다. 풀이는 다음 두 가지 방법으로 접근하여 보았다. 투 포인터 알고리즘: 두 개의 포인터를 이용하여 연속된 수들의 합을 관리. start와 end 두 포인터를 동시에 이동시키면서 그 사이의 합과 n이 어떻게 비교되는지를 확인. 합이 n보다 작다면 end를 증가시키고, n과 같다면 카운트를 증가시킨 후 start를 증가시키고, n보다 크다면 start를 증가. 브루트 포스 알고리즘: 가능한 모든 연속된 수열을 검사하며 그 합이 n인 경우를 찾음. 두 방법 모두 적절히 활용한다면 문제를 해결할..

문제 설명 제한 사항 및 입출력 예제 개념 1과 0으로 구성된 문자열에서 특정 조건을 만족할 때까지 이진 변환 프로세스를 반복하는 문제다. 프로세스는 다음과 같다. 문자열에서 0을 제거 (제거한 횟수 카운트) 문자열의 길이를 이진법으로 표현 (입력 문자열이 1이 될때까지, 횟수 카운트) 이때 문자열의 길이를 이진법으로 표현하기 위해 bitset 라이브러리를 사용하면 효율적으로 문제를 풀 수 있다. 풀이 #include #include #include using namespace std; vector solution(string s) { vector answer(2); int cnt = 0; while (s[0] != '1' || s.size() != 1) { int num = count(s.begin()..

그래프 컬러링개요　그래프 컬러링(graph coloring) 문제는 주어진 그래프에서 서로 인접한 정점끼리 같은 색을 갖지 않도록 모든 정점에 색상을 지정하는 것이다. 이때 에지의 가중치는 사용하지 않는다. 컬러링의 주요 종류는 다음과 같다. 정점 컬러링: 가장 기본적인 형태의 그래프 컬러링. 인접한 정점들은 다른 색깔을 가져야 한다는 규칙을 따름.에지 컬러링: 각 에지를 색칠하는 데 중점을 두며, 어떤 두 에지도 같은 색깔을 가질 수 없음. 이 규칙은 에지가 공유하는 정점에도 적용됨.착색수(chromatic number): 그래프를 적절히 색칠하는 데 필요한 최소 색깔 수 (NP-완전 문제) 　그래프 컬러링은 택시 예약 스케줄 작성, 스도쿠 퍼즐 풀기, 시험 시간표 작성 등을 그래프로 모델링한 후 컬러..

문제 설명 제한 사항 및 입출력 예제 개념 두 수열 A와 B의 각 원소를 한 번씩 곱한 값을 더했을 때, 그 합이 최소가 되도록 만드는 문제다. 즉, 한 수열에서 최솟값을 다른 수열에서의 최댓값과 곱하는 과정을 반복하여 합을 최소화하는 것이 목표다. 이를 구현하는 방법은 여러 가지가 있다. 풀이 (1) multiset 활용 #include #include using namespace std; int solution(vector A, vector B) { int answer = 0; multiset ms1(A.begin(), A.end()), ms2(B.begin(), B.end()); while (!ms1.empty()) { answer += (*ms1.begin() * *ms2.rbegin()); ms..

시간 복잡도　지난 포스팅에서 디스조인트-셋 자료구조를 사용하면 시간 복잡도가 O(Ea(V))로 줄어들며, 정점이 많은 그래프에서 큰 성능 차이가 발생한다고 하였다. 이는 디스조인트-셋 데이터 구조에 특정 휴리스틱을 적용했다는 것을 의미하는데, 여기서 휴리스틱(heuristics)이란 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 사용하는 어림짐작의 기술, 즉 항상 최적의 해를 보장하진 않지만 신속하게 답을 구할 수 있는 접근 방식이다. 이 휴리스틱은 Union by rank와 Path compression이다. 　Union by rank는 두 트리를 합칠 때 더 작은 랭크(rank)의 트리를 더 큰 랭크의 트리 아래에 두는 방법이고, Path compression은 find 연산을 수행할 ..

문제 설명 제한 사항 및 입출력 예제 개념 공백으로 구분된 문자열에서 최솟값과 최댓값을 뽑아 출력하는 문제다. 공백을 만날 때마다 벡터에 문자열을 정수로 바꾼 후 값을 넣어주는 방식을 사용하면 된다. 풀이 #include #include #include using namespace std; string solution(string s) { string tmp; vector v; int max, min; for (const auto& str : s) { if (str != ' ') tmp += str; else { v.push_back(stoi(tmp)); tmp = ""; } } v.push_back(stoi(tmp)); min = *min_element(v.begin(), v.end()); max = ..

문제 설명 제한 사항 및 입출력 예제 개념 대괄호가 올바르게 짝지어졌는지 확인하는 문제다. 스택을 사용하는 대표적인 문제로서 특정 조건을 만족할 때 스택에서 문자를 뽑아서 스택이 비었는지 여부를 체크하면 쉽게 해결할 수 있다. 풀이 #include #include #include using namespace std; bool solution(string s) { stack st; bool answer = true; for (const auto& ch : s) { if (st.empty()) st.push(ch); else if (st.top() == '(' && ch == ')') st.pop(); else st.push(ch); } if (!st.empty()) answer = false; return..

최소 신장 트리 문제그리디 알고리즘 요구 조건　앞 절에서 모든 문제에 그리디 방식을 적용할 수 있는 것은 아니라고 했다. 즉, 최적 부분 구조(optimal substructure)와 그리디 선택(greedy choice)이라는 두 가지 속성을 모두 갖는 문제만 그리디 접근 방식으로 최적의 솔루션을 구할 수 있다.  　최적 부분 구조는 큰 문제의 최적해가 부분 문제의 최적의 해답들로 구성될 수 있는 구조를 의미한다. 그리디 선택 속성은 현재의 선택이 미래의 선택에 영향을 미치지 않고, 각 단계에서 최적의 선택을 하면 전체적으로 최적의 해답을 얻을 수 있는 것을 의미한다. 　이러한 특성에 대해 이해하기 위해 크루스칼 최소 신장 트리 알고리즘에 대해 알아보도록 하자.개요　최소 신장 트리(Minimum Spa..

문제 설명 제한 사항 및 입출력 예제 개념 첫 문자를 대문자로 처리하고 나머지 알파벳을 소문자로 처리하는 문자열 처리 문제다. 입력 문자열에서 각 단어의 첫 문자를 대문자로, 그 외의 알파벳을 소문자로 바꾸는 작업이 필요하다. 여기서 '단어'는 공백 문자로 구분되므로, 문자열을 순회하며 공백 문자를 만났을 때 그 다음 문자를 대문자로 바꿔주면 된다. 풀이 #include #include using namespace std; string solution(string s) { string answer; bool isTrue = false; answer += toupper(s[0]); s = s.substr(1); 공백 문자를 만났는지 여부를 체크할 플래그 변수 isTrue를 false로 초기화해준다. 그리고..

문제 설명 제한 사항 및 입출력 예제 개념 최댓값과 최솟값 모두 처리할 수 있는 이중 우선순위 큐를 구현하는 문제다. 최소힙과 최대힙을 나눠서 처리하는 방법과, 동일한 요소를 여러 번 저장하는 multiset 자료구조를 이용하는 방법 두 가지가 있다. 풀이 (1) 최소힙, 최대힙 #include #include #include #include using namespace std; vector solution(vector operations) { vector temp, answer; for (const auto& str : operations) { string tmp = str.substr(2); if (str[0] == 'I') temp.push_back(stoi(tmp)); else { if (tmp ..