<본 카테고리는 "코딩 테스트를 위한 자료 구조와 알고리즘 with C++을 기반으로 작성하였습니다>
시간 복잡도
지난 포스팅에서 디스조인트-셋 자료구조를 사용하면 시간 복잡도가 O(Ea(V))로 줄어들며, 정점이 많은 그래프에서 큰 성능 차이가 발생한다고 하였다. 이는 디스조인트-셋 데이터 구조에 특정 휴리스틱을 적용했다는 것을 의미하는데, 여기서 휴리스틱(heuristics)이란 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 사용하는 어림짐작의 기술, 즉 항상 최적의 해를 보장하진 않지만 신속하게 답을 구할 수 있는 접근 방식이다. 이 휴리스틱은 Union by rank와 Path compression이다.
Union by rank는 두 트리를 합칠 때 더 작은 랭크(rank)의 트리를 더 큰 랭크의 트리 아래에 두는 방법이고, Path compression은 find 연산을 수행할 때, 검사한 노드들이 모두 직접 대표 노드를 가리키도록 만드는 방법이다. 이 두 휴리스틱을 적용하면, 각 연산의 복잡도는 거의 상수에 가까워진다. 따라서 알고리즘이 각 에지에 대해 일정한 작업을 수행하되, 그 작업의 복잡도가 아주 느리게 증가하므로 OE(a(V))가 된다.
예시
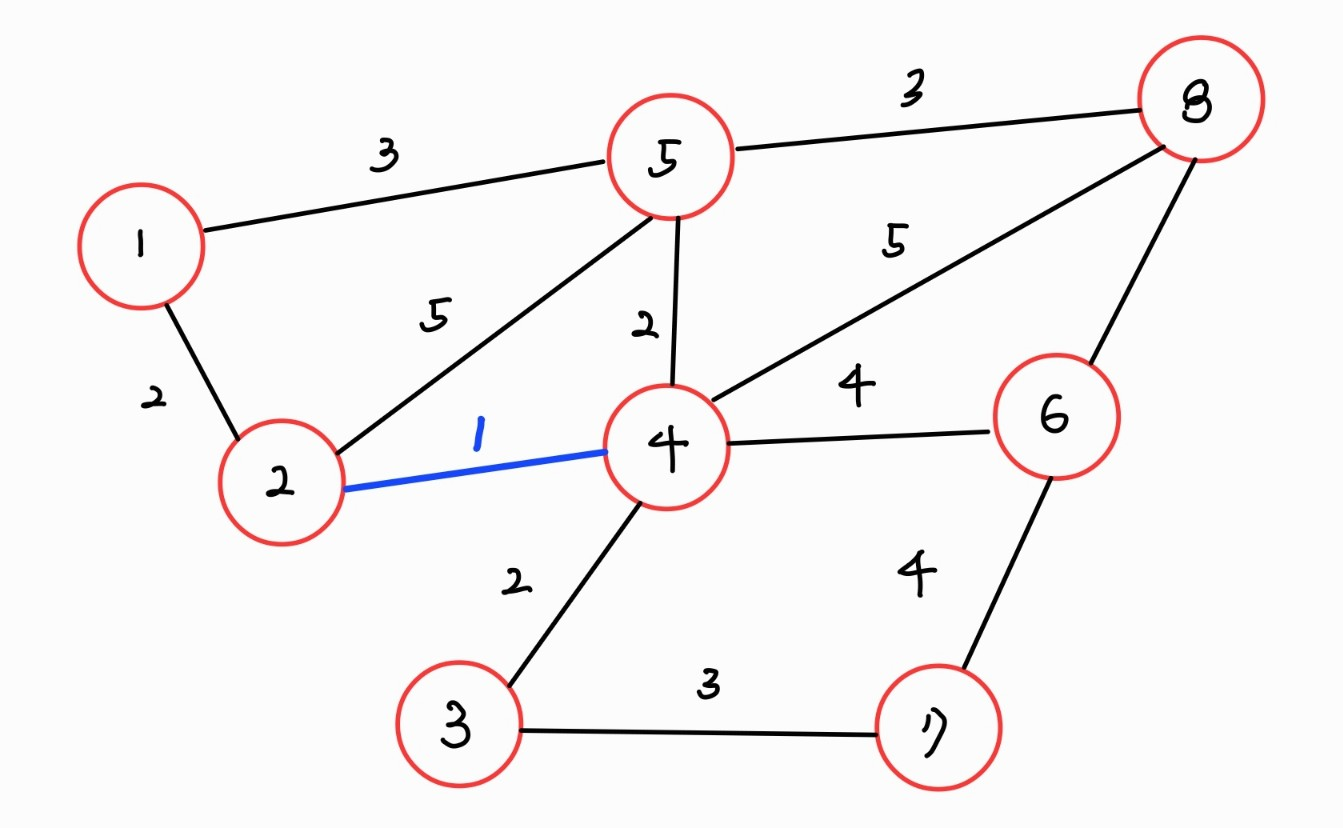
다음과 같은 그래프가 있다고 가정해 보자.


여기서 weight가 가장 작은 에지를 MST에 추가한다. 가중치가 가장 작은 것은 2와 4를 연결하는 에지이므로 (2,4) 에지가 선택되었고, DS에서는 union(2,4)가 수행된다.
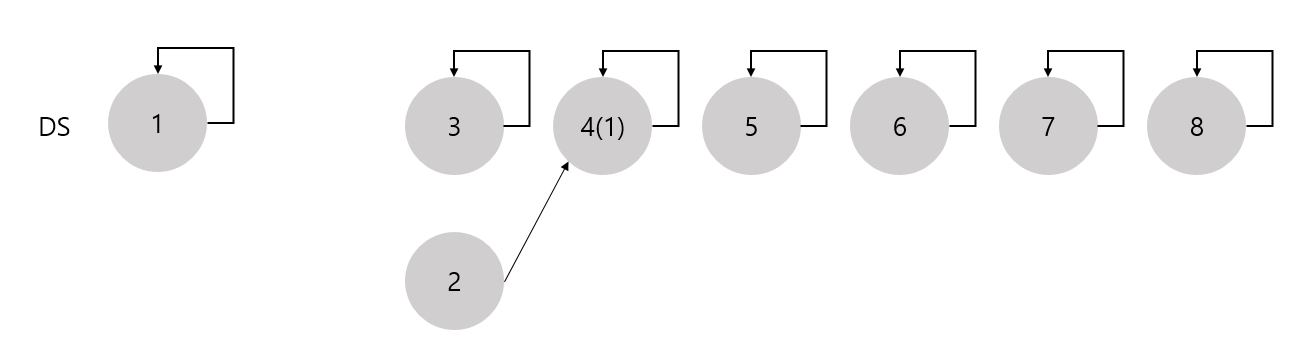
그 후 가중치가 작은 순대로 에지를 추가하다 보면, (1,5) 에지를 검토할 차례가 나타난다. 해당 상황을 보면 다음과 같다.


1번과 5번 정점이 이미 같은 트리에 존재하고 있다. 따라서 (1,5) 에지를 연결하면 사이클이 발생하기 때문에 (1,5) 에지를 MST에 추가할 수 없다. 이러한 방식으로 추가하면 MST에는 다음과 같은 그래프가 남게 된다.
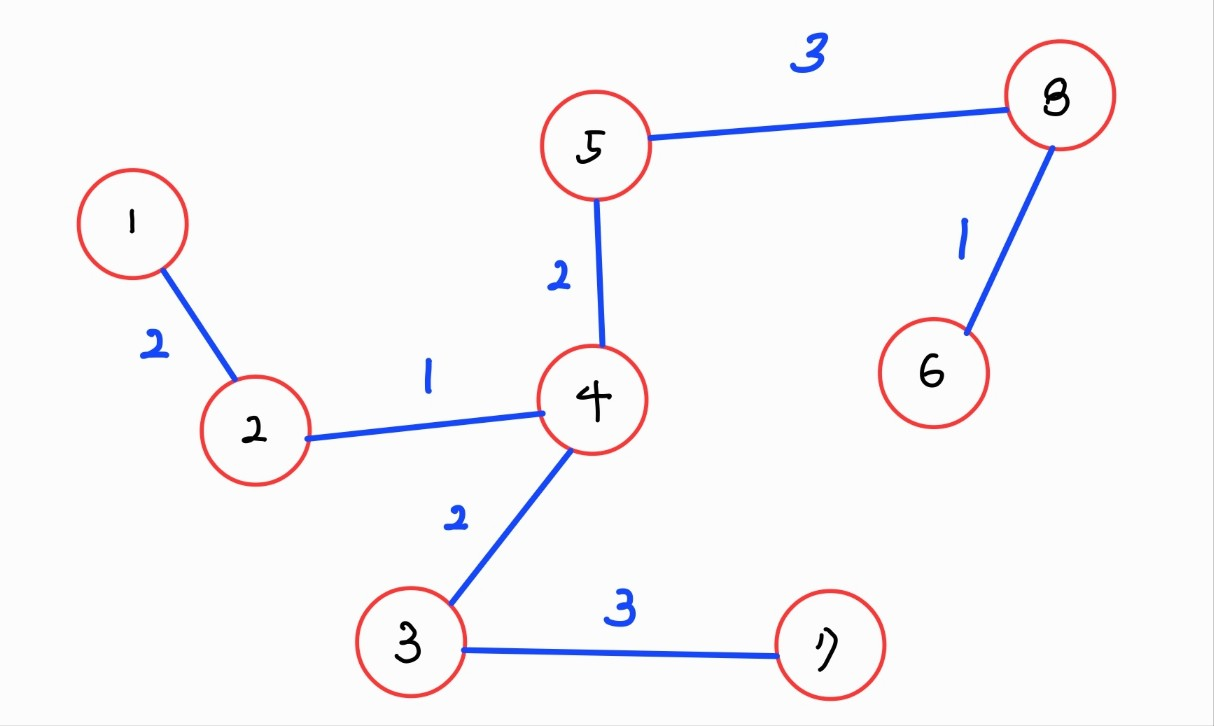
구현
#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <queue>
using us = unsigned;
struct node
{
us _id, _rank, _parent;
node(us id) : _id(id), _rank(0), _parent(id)
{
}
};Disjoint-set을 만들기 위해 node 구조체를 선언해 놓는다. 해당 노드에는 id와 트리의 높이를 나타내는 rank, 부모를 가리키는 정보를 갖고 있어야 하고, 추후에 생성자를 이용해 초기화하기 위해 node(us id) 생성자 함수도 추가해 놓자.
class ds
{
std::vector<node> _nodes;
public:
ds(us n)
{
_nodes.reserve(n);
}
void make_set(us x)
{
_nodes.push_back(x);
}
us find(us x)
{
auto it = std::find_if(_nodes.begin(), _nodes.end(), [x](auto n)
{
return n._id == x;
});
us id = (*it)._id;
while (id != _nodes[id]._parent)
id = _nodes[id]._parent;
return id;
}
void union_set(us x, us y)
{
auto root_x = find(x);
auto root_y = find(y);
if (root_x == root_y)
return;
if (_nodes[root_x]._rank > _nodes[root_y]._rank)
std::swap(root_x, root_y);
_nodes[root_x]._parent = _nodes[root_y]._parent;
_nodes[root_y]._rank++;
}
};
Disjoint-Set 자료 구조를 구현할 ds 클래스다. x를 ID로 갖는 원소를 새로운 집합으로 생성하는 make_set() 함수와, 원소 x가 속한 집합의 대표 원소를 찾는 find() 함수, 두 개의 원소 x와 가 속한 집합을 합치는 union_set() 함수를 구현해 놓았다.
struct edge
{
us _src, _dst, _weight;
};
class graph
{
us _v;
std::vector<edge> _list;
public:
graph(us n) : _v(n)
{
}
us vertices() const
{
return _v;
}
auto& edges() const
{
return _list;
}
auto edges(us v) const
{
std::vector<edge> edge_from_v;
for (const auto& e : _list)
{
if (e._src == v)
edge_from_v.push_back(e);
}
return edge_from_v;
}
void add_edge(edge&& e)
{
if (e._src >= 1 && e._src <= _v && e._dst >= 1 && e._dst <= _v)
_list.push_back(e);
else
std::cerr << "Invalid range vertex\n";
}
};그래프 구조를 구현한 graph 클래스와, 에지 구조를 표현한 edge 구조체다. 에지는 출발지점 _src와 도착지점 _dst, 그리고 가중치 _weight로 구성되어 있다.
그래프 클래스는 정점의 개수 _v와 모든 에지들을 저장할 벡터 _list를 멤버 변수로 갖는다. 또한 정점의 개수를 반환하는 함수 vertices(), 정점 v에서 나가는 에지를 반환하는 edges() 함수, 이를 오버로딩하여 전체 에지 리스트를 반환하는 auto& edges() 함수, 에지를 추가하는 add_edge() 함수로 구성되어 있다. 이때 add_edge() 함수에서 edge&& e를 인자로 받는 이유는 rvalue 참조를 통해 에지 객체를 복사하지 않고, 임시 객체의 소유권을 직접 이동하게 하는 것(move semantics)을 의미한다.
- edge& e를 인자로 쓰면 lvalue 참조가 되어 객체의 복사본이 만들어지지 않고, 이동 시맨틱이 적용되지 않는다.
graph MST(const graph& g)
{
std::priority_queue<edge, std::vector<edge>, std::greater<edge>> heap;크루스칼 최소 신장 트리 알고리즘을 구현할 MST() 함수다. 여기서 에지를 기준으로 최소힙을 구현할 건데, 에지에 대한 정렬 기준이 잡혀있지 않으므로 연산자 오버로딩을 적용해야 한다.
struct edge
{
us _src, _dst, _weight;
bool operator < (const edge& e) const
{
return this->_weight < e._weight;
}
bool operator > (const edge& e) const
{
return this->_weight > e._weight;
}
};따라서 다음과 같이 < 연산자와 > 연산자를 수정해 주자.
graph MST(const graph& g)
{
std::priority_queue<edge, std::vector<edge>, std::greater<edge>> heap;
for (const auto& e : g.edges())
heap.push(e);
us size = g.vertices();
ds dset(size);
for (us i = 0; i < size; ++i)
dset.make_set(i);
graph mst(size);
while (!heap.empty())
{
auto e = heap.top();
heap.pop();
if (dset.find(e._src) != dset.find(e._dst))
{
mst.add_edge(edge{ e._src, e._dst, e._weight });
dset.union_set(e._src, e._dst);
}
}
return mst;
}다시 MST 함수로 돌아오자. 힙에 에지를 삽입하고, 디스조인트-셋 자료 구조를 힙의 크기에 맞게 초기화해 주자. 이 자료 구조를 이용하여 최소 힙에서 최소 가중치 에지를 추출하여 선택한 에지가 사이클을 생성하지 않는지 판단한 후에 에지를 MST에 추가하면 된다.
int main()
{
std::map<us, std::vector<std::pair<us, us>>> m;
graph g(9);
m[1] = { {2, 2}, {5, 3} };
m[2] = { {1, 2}, {5, 5}, {4, 1} };
m[3] = { {4, 2}, {7, 3} };
m[4] = { {2, 1}, {3, 2}, {5, 2}, {6, 4}, {8, 5} };
m[5] = { {1, 3}, {2, 5}, {4, 2}, {8, 3} };
m[6] = { {4, 4}, {7, 4}, {8, 1} };
m[7] = { {3, 3}, {6, 4} };
m[8] = { {4, 5}, {5, 3}, {6, 1} };
for (const auto& i : m)
{
for (const auto& j : i.second)
g.add_edge(edge{ i.first, j.first, j.second });
}
graph ans = MST(g);
auto edges = ans.edges();
std::sort(edges.begin(), edges.end(), [](const edge& a, const edge& b) {
return a._src < b._src;
});
us last_src = 0;
for (const auto& e : edges) {
if (last_src != e._src) {
std::cout << "\n";
last_src = e._src;
}
std::cout << "{" << e._src << ", " << e._dst << ", " << e._weight << "}, ";
}
}
총합본
#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <queue>
using us = unsigned;
struct node
{
us _id, _rank, _parent;
node(us id) : _id(id), _rank(0), _parent(id)
{
}
};
class ds
{
std::vector<node> _nodes;
public:
ds(us n)
{
_nodes.reserve(n);
}
void make_set(us x)
{
_nodes.push_back(x);
}
us find(us x)
{
auto it = std::find_if(_nodes.begin(), _nodes.end(), [x](auto n)
{
return n._id == x;
});
us id = (*it)._id;
while (id != _nodes[id]._parent)
id = _nodes[id]._parent;
return id;
}
void union_set(us x, us y)
{
auto root_x = find(x);
auto root_y = find(y);
if (root_x == root_y)
return;
if (_nodes[root_x]._rank > _nodes[root_y]._rank)
std::swap(root_x, root_y);
_nodes[root_x]._parent = _nodes[root_y]._parent;
_nodes[root_y]._rank++;
}
};
struct edge
{
us _src, _dst, _weight;
bool operator < (const edge& e) const
{
return this->_weight < e._weight;
}
bool operator > (const edge& e) const
{
return this->_weight > e._weight;
}
};
class graph
{
us _v;
std::vector<edge> _list;
public:
graph(us n) : _v(n)
{
}
us vertices() const
{
return _v;
}
auto& edges() const
{
return _list;
}
auto edges(us v) const
{
std::vector<edge> edge_from_v;
for (const auto& e : _list)
{
if (e._src == v)
edge_from_v.push_back(e);
}
return edge_from_v;
}
void add_edge(edge&& e)
{
if (e._src >= 1 && e._src <= _v && e._dst >= 1 && e._dst <= _v)
_list.push_back(e);
else
std::cerr << "Invalid range vertex\n";
}
};
graph MST(const graph& g)
{
std::priority_queue<edge, std::vector<edge>, std::greater<edge>> heap;
for (const auto& e : g.edges())
heap.push(e);
us size = g.vertices();
ds dset(size);
for (us i = 0; i < size; ++i)
dset.make_set(i);
graph mst(size);
while (!heap.empty())
{
auto e = heap.top();
heap.pop();
if (dset.find(e._src) != dset.find(e._dst))
{
mst.add_edge(edge{ e._src, e._dst, e._weight });
dset.union_set(e._src, e._dst);
}
}
return mst;
}
int main()
{
std::map<us, std::vector<std::pair<us, us>>> m;
graph g(9);
m[1] = { {2, 2}, {5, 3} };
m[2] = { {1, 2}, {5, 5}, {4, 1} };
m[3] = { {4, 2}, {7, 3} };
m[4] = { {2, 1}, {3, 2}, {5, 2}, {6, 4}, {8, 5} };
m[5] = { {1, 3}, {2, 5}, {4, 2}, {8, 3} };
m[6] = { {4, 4}, {7, 4}, {8, 1} };
m[7] = { {3, 3}, {6, 4} };
m[8] = { {4, 5}, {5, 3}, {6, 1} };
for (const auto& i : m)
{
for (const auto& j : i.second)
g.add_edge(edge{ i.first, j.first, j.second });
}
graph ans = MST(g);
auto edges = ans.edges();
std::sort(edges.begin(), edges.end(), [](const edge& a, const edge& b) {
return a._src < b._src;
});
us last_src = 0;
for (const auto& e : edges) {
if (last_src != e._src) {
std::cout << "\n";
last_src = e._src;
}
std::cout << "{" << e._src << ", " << e._dst << ", " << e._weight << "}, ";
}
}
요약
최소 신장 트리 알고리즘
1. 정의: 모든 정점을 연결하고 연결된 에지의 가중치 합이 최소인 트리 T를 구하는 알고리즘
2. 특징
a. 그리디 알고리즘으로 해결 가능
- 최적 부분 구조, 그리디 선택 만족
b. 크루스칼 최소 신장 트리 알고리즘이 대표적
- 디스조인트-셋 자료 구조를 채택하여 시간 복잡도를 O(Ea(V))로 줄일 수 있음.
- 이외에는 O(E logE)
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 순회 문제 (0) | 2023.06.14 |
|---|---|
| [알고리즘] 그리디 알고리즘 - 그래프 컬러링 (0) | 2023.05.30 |
| [알고리즘] 그리디 알고리즘 - 최소 신장 트리 문제 (1) (0) | 2023.05.27 |
| [알고리즘] 그리디 알고리즘 - 배낭 문제 (0) | 2023.05.23 |
| [알고리즘] 그리디 알고리즘 - 개요 및 최단 작업 우선 스케줄링 (0) | 2023.05.22 |