주파수 영역에서의 필터링
개요
지난 시간까지는 이미지에 푸리에 변환을 적용하기 위한 기초적인 이론들을 배웠었다. 그리고 이미지에 푸리에 변환을 적용했을 때 어떻게 되는지도 간단한 실습을 통해 확인할 수 있었다. 이번 시간에는 필터링을 하기 위한 조건들에 대해 배워보도록 하겠다.
본문
Nyquist-Shannon Sampling Theroem


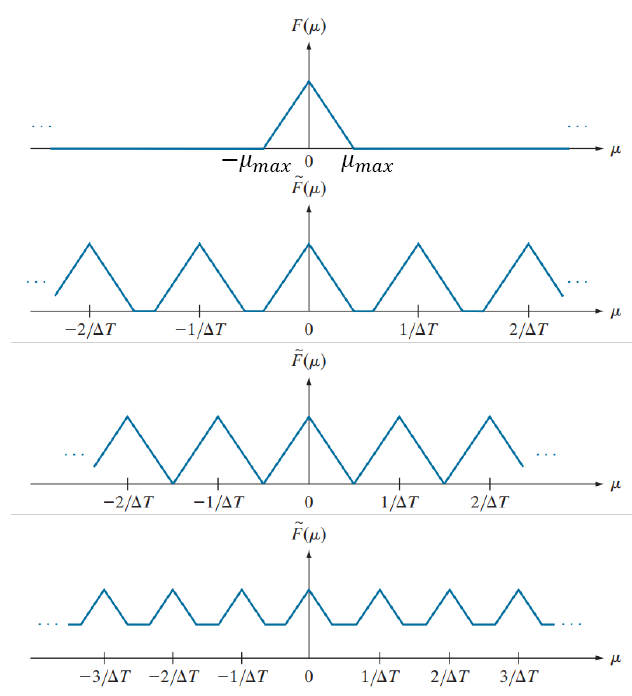
푸리에 변환을 적용한 주기적인 임펄스 열은 위의 수식이 나온다고 했었다. 샘플링 간격 △T는 연속적인 신호를 디지털 신호로 변환할 때 신호를 정확하게 복원할 수 있는지를 결정한다. 이러한 대역 제한 신호(Bandlimited Signal)에 대해, Nyquist-Shannon 샘플링 정리는 연속 신호를 디지털로 변환할 때 필요한 최소 샘플링 속도를 정의한다. 즉, 샘플링 속도는 신호의 최대 주파수의 두 배 이상이어야 한다.
- 여기서 Bandlimited가 되어 있어야 샘플링이 가능하다. 즉, 주기적인 신호가 고립되어 있어야 한다.
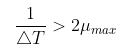
이 정리에 따르면, 신호의 최대 주파수의 두 배 이상을 샘플링하는 것을 Over-sampling, 정확히 두 배를 샘플링하는 것을 Critically-sampling, 두 배 미만을 샘플링하는 것을 Under-sampling이라고 한다. Under-sampling의 경우, 신호의 고주파수 성분이 손실되어 복원이 불가능해진다.
- 하지만 Critically-sampling은 이상적인 LPF를 설계하기 힘들기 때문에 실제로 적용하기 힘들다.
Aliaisng

앞서 Nyquist의 샘플링 이론에 따르면 최대 주기의 2배보다 작은 경우, Under-sampling이 발생하며 신호를 복원할 수 없는 상태가 된다고 하였다. 이러한 현상을 에일리어싱(Aliasing)이라고 한다. 그렇다면 이미지에서 에일리어싱이 일어나면 어떻게 될까? 그리고 이를 제거하려면 어떻게 해야 할까?

다음과 같은 32x32 이미지(좌)가 주기적으로 96x96(우) 크기로 있고, 샘플링 주파수는 한 픽셀 별로 밝기 정보를 갖고 있으므로 1이라고 해보자. 즉, 동일한 이미지를 멀리서 찍으면 왼쪽처럼 격자가 여러 번 보일 것이고, 가까이에서 찍으면 오른쪽처럼 보일 것이다. 이를 조금 더 멀리서 찍으면 다음과 같이 격자가 깨지는 부분이 생긴다.

이러한 현상을 주파수의 관점에서 분석해 보면 Ailasing이 발생한다는 것을 알 수 있다. 왼쪽의 그림은 주기가 1.8 픽셀이므로 주파수가 1/1.8 = 0.55Hz가 된다. 즉, 최대 주파수가 1.1이 되므로 원본 신호를 복원할 수 없는 부분이 발생하는 것이다.
반면 오른쪽 그림은 주기가 0.9596 픽셀이므로 주파수가 1/0.9596 = 1.0421Hz가 된다. 즉, 최대 주파수가 2.0842가 되므로 이 또한 원본 신호를 복원할 수 없게 된다. 여기서 왼쪽 그림처럼 촘촘하게 나오지 않고, 마치 주기가 32픽셀인 것처럼 큼지막하게 나오는데 이는 작게 찍힌 점들이 하나로 뭉쳐서 다시 검은색/흰색 사각형이 된 것처럼 보이는 것이다.
실습
I = imread("zone_plate.jpg");
figure(1);
imshow(I); truesize;
sampling = 2;
[H W] = size(I);
Ir = [];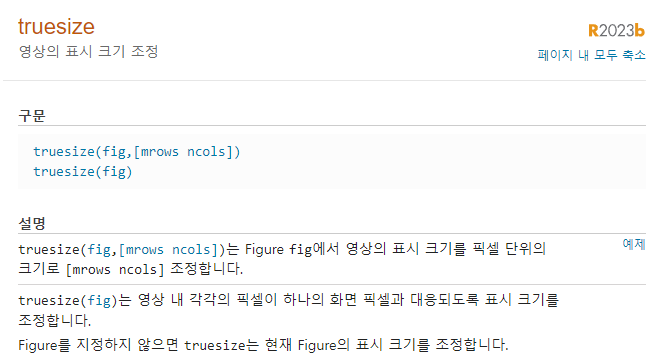

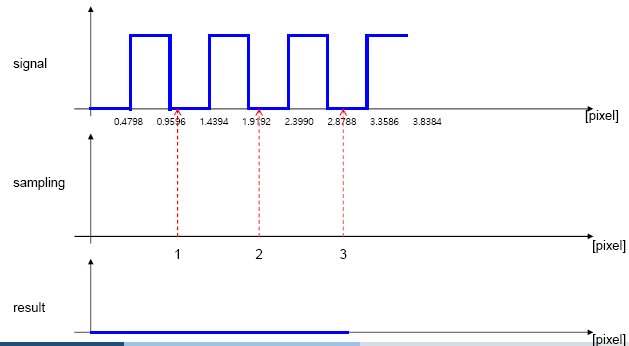
다음과 같은 이미지를 이용해 에일리어싱 현상을 관찰해 보자. 여기서 truesize는 정확한 샘플링을 위해 이미지의 크기를 픽셀 단위로 지정하려고 사용하였다. 또한 에일리어싱을 확인하기 위해 이미지의 주파수를 변경하는 인자 sampling을 2로 초기화하였다.
for i = 1:sampling:H
for j = 1:sampling:W
Ir(floor(i/sampling)+1, floor(j/sampling)+1) = I(i,j);
end
end
figure(2);
imagesc(Ir); colormap gray; truesize;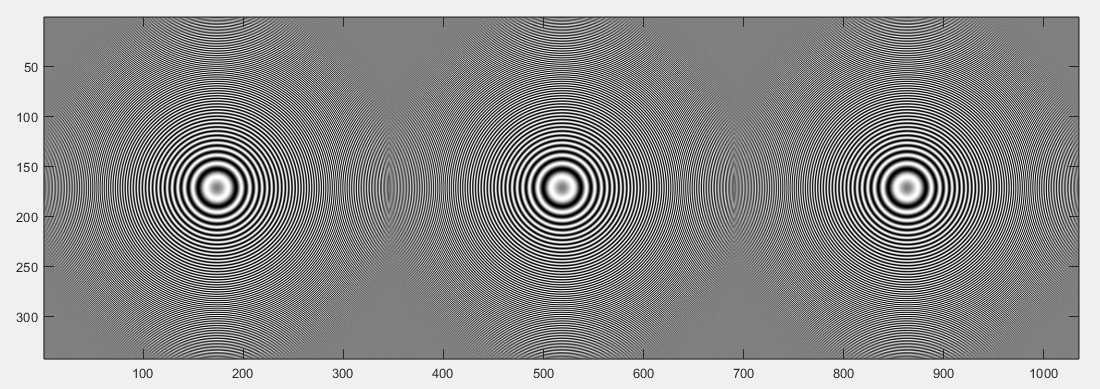
원본 이미지 I에서 샘플링 간격으로 픽셀을 선택하고, 이를 새 배열 Ir에 할당하게 코드를 작성하였다. 이 과정은 이미지의 해상도를 변경하는 리샘플링, 그중에서 해상도를 낮추는 다운 샘플링 과정이다. 그 후 나서 이미지를 출력하면 동심원 형태가 일그러지는 것을 확인할 수 있다. 이러한 현상은 원래 패턴이 빠르게 변화하고 있는데, 샘플링하는 주파수가 따라가지 못해서 발생하는 것이다.
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Filtering in Frequency Domain (3) (0) | 2024.01.20 |
|---|---|
| [디지털영상처리] Filtering in Frequency Domain (2) (2) | 2024.01.04 |
| [디지털영상처리] Fourier Theory (2) (0) | 2023.11.18 |
| [디지털영상처리] Fourier theory (1) (0) | 2023.11.16 |
| [디지털영상처리] Image Sharpening (3) (0) | 2023.11.10 |