푸리에 이론
개요

이미지에서 주파수(Frequency)는 이미지의 공간적 변화가 얼마나 빠르게 발생하는지를 나타내는 척도다. 이미지에서 이것은 일반적으로 픽셀 간의 밝기 변화의 정도로 표현되며, 이는 이미지의 세부 사항과 가장자리의 고주파수 성분과, 부드러운 영역의 저주파수 성분으로 구분된다.
이번 시간에는 시간 도메인에서의 이미지가 아닌, 주파수 도메인에서 이미지를 다루기 위해 필요한 푸리에 변환 이론을 배워보도록 하자.
본문
푸리에 이론을 쓰는 이유

푸리에 이론(Fourier Theory)은 일반적으로 시간 영역에서 다루기 힘든 내용을 주파수 영역으로 넘겨서 해결할 때 사용한다. 예를 들어, 시간 도메인에서 이미지에 필터를 적용하는 컨볼루션은 각 입력 샘플에 대해 커널의 모든 값과 곱셈을 수행한 후, 그 결과를 더하므로 계산량이 많은 작업이다. 하지만 주파수 영역에서 컨볼루션은 단순한 곱셈으로 수행될 수 있어, 훨씬 빠르고 효율적이다.
또한 시간 영역에서 노이즈는 이미지 전반에 걸쳐 불규칙하게 분포하며, 이를 직접 제거하는 필터를 씌우는 등 여러 과정을 거쳐야 한다. 하지만 주파수 영역에서 노이즈는 고주파 성분으로 나타나므로, Low Pass Filter를 적용하기만 하면 쉽게 제거할 수 있다.
푸리에 급수
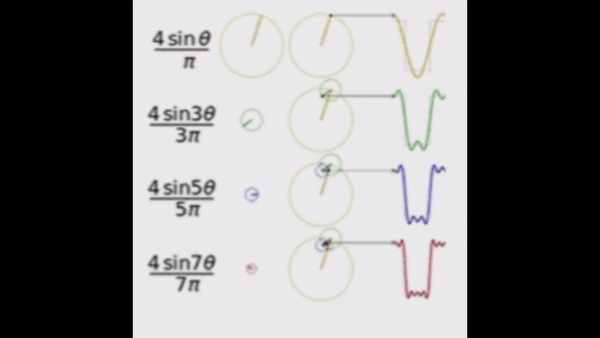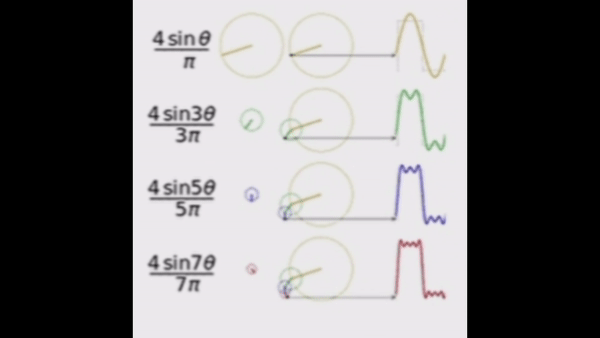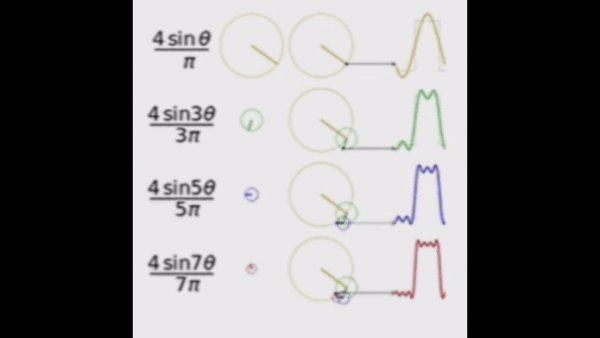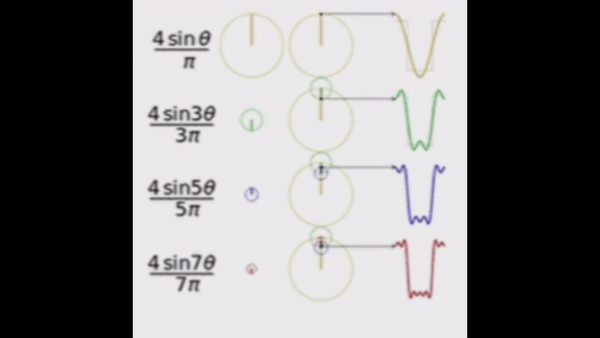
푸리에 이론은 크게 푸리에 급수와 푸리에 변환으로 나눌 수 있다. 먼저 푸리에 급수(Fourier Series)는 주기적인 함수를 사인과 코사인 함수의 무한 합으로 표현하는 방법이다. 물리적으로 접근하면, 주기적 신호나 파동의 주파수 성분을 분해하여 각 주파수에서의 진폭과 위상을 나타내는 것이다. 이는 주기 함수가 다음과 같은 성질을 갖고 있기 때문에 가능하다.

즉, 기본 주기(Fundamental Period) T에 정수 n배를 더한 시간에서의 함숫값은 원래 시간 t에서의 함숫값과 동일하다. 예를 들어, 기본 주기가 2π인 f(t) = cos(t)를 생각해 보자. f(t + nT) = cos(t _ n * 2π)를 살펴 보면, 코사인 함수의 주기성 때문에 n*2π만큼 x에 더해도 함수의 값은 변하지 않는다. 이는 코사인 함수는 2π의 배수만큼 이동해도 원래의 값과 같기 때문이다.
하지만 특정한 주기를 가지고 있는 함수들은 n이 분수의 형태여도 동일한 성질을 갖는다. 예를 들어, 코사인파 함수를 다음과 같이 정의해 보자.

여기서 4pi/T는 각주기를 나타내며, 코사인과 사인 함수가 2π 주기를 갖기 때문에, 이를 곱함으로써 주기를 T로 조정하기 위해 다음과 같이 설정하였다. 앞서 코사인 함수는 주기 함수이므로 함수 f(t)에 t+T를 넣으면 성립한다는 것은 이미 알고 있다. 따라서 f(t)에 t+T/2를 대입했을 때 f(t)와 같은 값인지만 확인하면 된다.
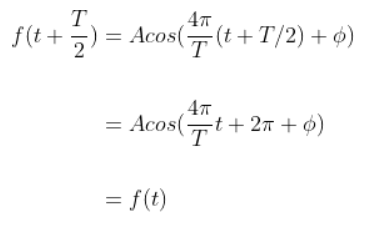
이제 이러한 주기 함수들을 이용하는 푸리에 급수의 아이디어를 알아보자. 기본 아이디어는 주기 T를 갖는 임의의 주기 함수 f(t)에 대해, 삼각함수의 무한 선형 결합으로 표현할 수 있다는 것이다. 이를 수식으로 표현하면 다음과 같다.

하지만 우리는 삼각 함수를 주로 다룰 것이므로, 주기가 2π가 되도록 fn(t)를 다음과 같이 정의하자.

따라서 임의의 주기 함수를 삼각함수의 무한 합으로 표현하는 푸리에 급수를 나타내면 다음과 같다. 이때 n은 0, +1, -1, +2, -2, .. 와 같은 정수다. 이를 이용해 구한 cn을 푸리에 계수(Fourier Coefficient)라고 한다.

이러한 내용을 기반으로, 주기 함수인 사인파를 사각파로 만드는 것을 시뮬레이션해보자.
figure(1);
t = 0:.02:4*pi;
x = zeros(size(t));
for i = 1:2:19
x = x + sin(i * t) / i;
y = x;
plot(t,y);
pause(1);
end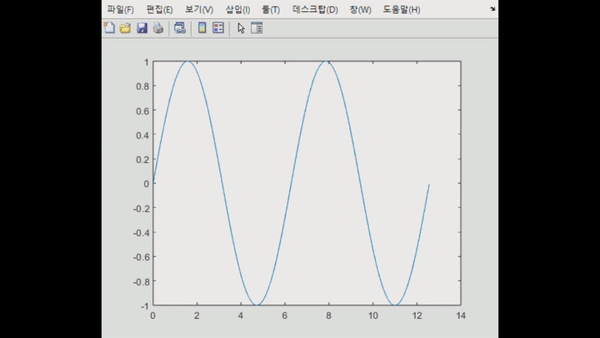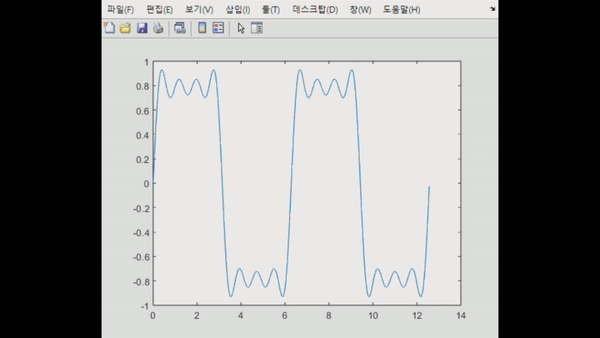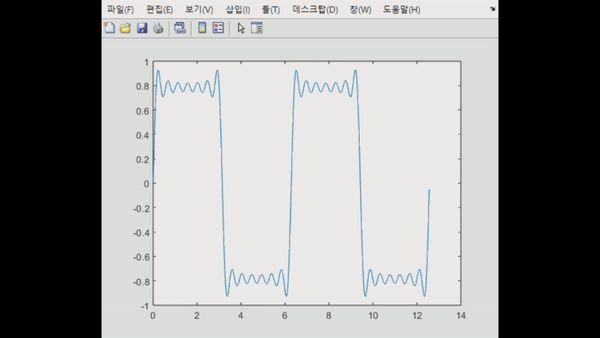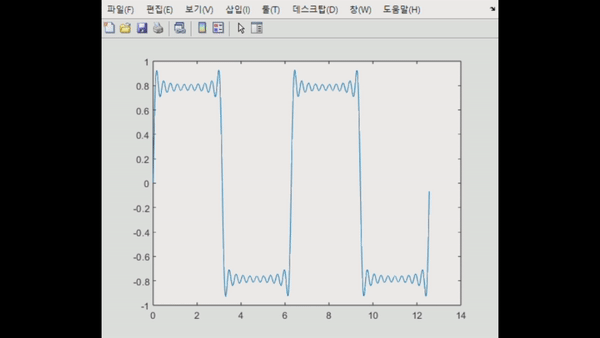
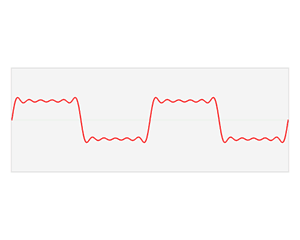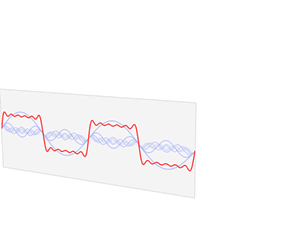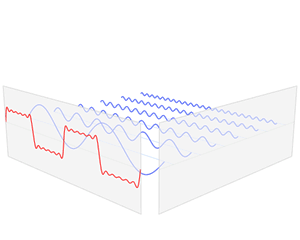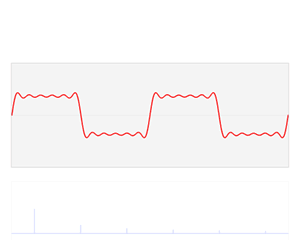
해당 코드는 k = 0부터 9까지 sin(2k+1)t / (2k+1)의 합을 구한 것이다. 확실히 주기적인 사인파들이 합쳐지니 사각파로 되는 것을 관찰할 수 있다.
푸리에 변환 (1): 임펄스의 특징
푸리에 변환을 알아보기에 앞서, 신호 처리를 위한 기본적인 지식부터 알아보자.

먼저 임펄스(Impulse)를 나타내는 디렉-델타(Dirac-delta) 함수다. 이 함수는 모든 실수에서 0의 값을 가지지만, 원점에서는 무한대로 발산하며, 그 총 적분은 1이다. 원점에서 포인트를 옮겨서 함수와 내적을 하면 그 자리에서 값이 나온다는 특징을 이용하여 샘플링을 할 때 사용된다.

즉, 해당 성질을 이용해 일정한 간격으로 나열된 일련의 델타 함수들인 임펄스 열(Impulse Train)은 연속 함수를 샘플링해서 이산적으로 만들 때 사용된다.

푸리에 변환 (2)

앞서 설명한 푸리에 급수는 주기적인 신호를 다루는 데 사용되지만, 푸리에 변환(Fourier Transform)은 비주기적인 신호까지 포괄하여 시간이나 공간의 함수를 주파수 성분으로 변환하는 데 사용된다. 이는 복잡한 신호나 함수를 기본 파동의 조합으로 분해하며, 특히 시간 도메인에서 신호 f(t)의 진폭이 A이고 각 주파수가 w일 때, 이 신호를 푸리에 변환하면 주파수 도메인에서 해당 진폭은 크기(Magitude)로, 각주파수는 위치로 나타나게 된다. 이를 통해 시간 도메인의 복잡한 형태의 신호가 주파수 영역에서는 각기 다른 주파수 성분으로 분해되어 분석할 수 있다.
이때 적분 식을 보면 알 수 있듯이, 비주기적인 함수를 범위를 무한대로 넓혀 주기 함수처럼 되게 하고 있다. 즉, 비주기적인 함수도 마치 무한한 주기를 가진 함수처럼 분해하여 각각의 주파수 성분으로 나타내고 있다.

다음과 같이 -W/2에서 W/2까지 A인 사각 펄스 함수에 푸리에 변환을 적용해 보자. 앞서 언급한 무한대의 적분을 주어진 주기에서 적분을 진행하면 수식은 다음과 같이 풀린다.
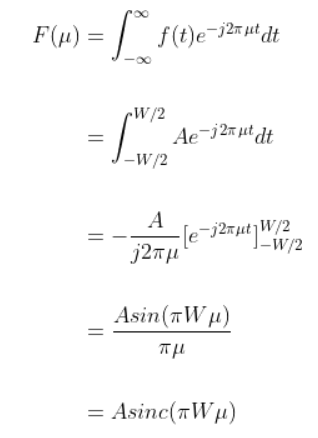
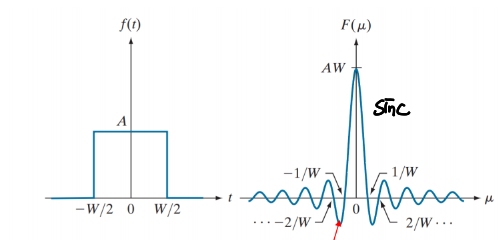
여기서 sinc함수는 아래 사진과 같이 x = 0에서 최댓값을 얻으며, x가 멀어질수록 함수는 진동하며 점차 감쇠하는 함수다.
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Filtering in Frequency Domain (1) (2) | 2023.12.07 |
|---|---|
| [디지털영상처리] Fourier Theory (2) (0) | 2023.11.18 |
| [디지털영상처리] Image Sharpening (3) (0) | 2023.11.10 |
| [디지털영상처리] Image Sharpening (2) (0) | 2023.11.07 |
| [디지털영상처리] Image Sharpening (1) (0) | 2023.11.06 |