Image Sharpening based on First-Order Derivatives and Summary
개요
이전까지 이미지 샤프닝을 위해 라플라시안과 같은 이차 미분 필터를 사용하거나, 원본 이미지로부터 LPF를 사용하여 흐릿한 이미지를 만든 다음 빼서 샤프닝 마스크를 만드는 Unsharp Masking을 사용하였다. 이차 미분을 이용한 방법은 세밀한 에지를 감지할 수 있으나, 노이즈에 민감하고, USM은 매개변수를 조절하여 샤프닝의 정도를 세밀하게 조정할 수 있으나, 계산 과정이 복잡하다는 단점이 있다.
이번 시간에는 수평과 수직 방향의 밝기 변화율을 측정하여 간단하고 빠른 계산을 보장하는 일차 미분을 이용한 샤프닝 필터에 대해 알아보도록 하겠다.
본문
원리
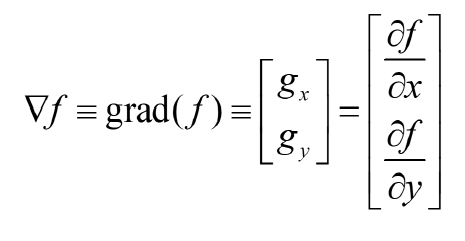
앞서 라플라시안을 설명할 때, Gradient 함수는 밝기 변화율을 측정한다고 했었다. 이러한 변화율은 x 방향과 y 방향의 픽셀 강도 변화량을 나타내며, 특히 에지 검출에 있어 중요한 역할을 한다. 여기서 에지는 픽셀 강도가 급격하게 변화하는 지점으로, 이미지 내에서 중요한 시각적 정보와 구조적 특징을 나타낸다. 이를 정량화하기 위해 우리는 Gradient의 크기를 사용해 다음과 같이 수식화할 수 있다.

제곱근 연산은 반복적인 계산 과정을 거쳐 정확한 값을 도출하는데, 이는 곱셉, 나눗셈, 제곱과 같은 복잡한 연산을 포함한다. 계산의 복잡성과 자원 소모를 줄이기 위해, 제곱근 대신 절댓값의 합으로 근사한다. 해당 근사가 가능한 이유는, 삼각 부등식에서 기인한다.

이렇게 함으로써 대량의 데이터를 처리하는 이미지 처리 작업에서 계산을 단순하게 해 주어 속도가 향상된다. 또한 실제 응용 분야에서 절댓값의 합이 제곱근을 사용하는 것과 유사한 결과를 가져오기도 한다. 특히 에지 감지와 같은 작업에서는 완벽한 정확성보다 에지의 위치와 대략적인 강도를 빠르게 파악하는 것이 더 중요할 수 있기 때문이다.

이렇게 차분을 한 번만 사용함으로써 이미지 샤프닝을 구현할 수 있다.
필터링 및 실습

일반적으로 많이 사용하는 일차 미분 필터를 알아보자. 먼저 소개할 것은 Roberts Cross-gradient Operator로, 가장 단순한 에지 검출 연산자다. 일반적으로 2x2 커널을 사용하여 이미지의 대각선 방향의 차이를 계산하여 미세한 에지를 감지하는 데 적합하다
I = rgb2gray(imread("dip_xe.jpg"));
gx = [1 0; 0 -1]; gy = [0 1; -1 0];
Ix = imfilter(I, gx, 'replicate', 'same');
Iy = imfilter(I, gy, 'replicate', 'same');
res = abs(Ix) + abs(Iy);
imshow(res);
Roberts 연산자의 커널은 다음과 같다.

따라서 gx와 gy를 각각 정의한 후, MATLAB에서 이미지에 필터를 적용하는 imfilter 함수를 사용하자. 주의할 점은 gx와 gy를 동시에 적용해서는 안 된다는 것이다. 만약 아래와 같이 필터를 동시에 적용한다면 결과가 어떻게 나올지 살펴보자.
I = rgb2gray(imread("dip_xe.jpg"));
gx = [1 0; 0 -1]; gy = [0 1; -1 0];
res = imfilter(I, abs(gx) + abs(gy), "replicate", "same");
imshow(res);이렇게 작성하면, gx와 gy에서의 -1이 절댓값 처리되어 1로 변하므로, 원하는 대각선 방향의 차이를 계산할 수 없게 된다. 올바른 방법은, 먼저 x 방향의 필터(gx)를 적용하고, 그다음 y 방향의 필터(gy)를 적용하여, 두 결과의 절댓값을 합산하는 것이다.
I = rgb2gray(imread("dip_xe.jpg"));
gx = [-1 -2 -1; 0 0 0; 1 2 1]; gy = [-1 0 1; -2 0 2; -1 0 1];
Ix = imfilter(I, gx, 'replicate', 'same');
Iy = imfilter(I, gy, 'replicate', 'same');
res = abs(Ix) + abs(Iy);
imshow(res);
이번엔 보다 정교한 에지 검출을 하는 Sobel Operator에 대해 알아보자. Sobel Operator의 커널은 다음과 같이 정의된다.

이 커널은 이미지를 가로지르는 수평 및 수직 에지를 감지하는 데 활용된다. 이때 이미지의 픽셀 간 변화율을 계산할 때 중앙 픽셀에 더 큰 가중치를 부여하기 위해 1 대신 2를 사용하였다. 즉, 중앙 행 또는 열의 변화가 주변값의 변화보다 두 배 더 중요하다고 가정한 것이다.
Roberts 연산자와 Sobel 연산자는 서로 다른 컨텍스트에서 사용된다. Roberts 연산자는 보다 미세한 에지를 감지하는 데 유용하지만, Sobel 연산자는 더 넓은 컨텍스트를 고려하여 부드럽고 노이즈에 강한 에지 검출이 가능하다.
매트랩 필터의 한계

주어진 내용을 바탕으로 필터를 적용하는 실습을 진행하다 보면, 코드는 동일하게 작성했는데 특정 이미지에서 예상하지 못한 동작이 발생할 때가 있다. 예를 들어 위의 이미지에 Sobel 필터를 적용해 보자.
I = rgb2gray(imread("ex.jpg"));
gx = [-1 -2 -1; 0 0 0; 1 2 1]; gy = [-1 0 1; -2 0 2; -1 0 1];
Ix = imfilter(I, gx, 'replicate', 'same');
Iy = imfilter(I, gy, 'replicate', 'same');
res = abs(Ix) + abs(Iy);
imshow(res);
분명 앞서 실습한 Sobel Operator와 동일한데, 에지 검출이 되다 말았다. 이는 매트랩에서 이미지를 처리하는 imfilter 함수가 uint8 형식을 쓰기 때문이다. 즉, 흰색 네모가 나와야 하는 부분에서 필터를 씌웠을 때 음수로 처리되는 부분이 있는데, uint8 형식은 음수를 0으로 saturation 하기 때문에 정보가 소실되는 부분이 발생하는 것이다. 그래서 imfiter의 출력을 double로 바꾸기 위해 myimfilter를 구현해 보았다.
I = rgb2gray(imread('ex.jpg'));
sobel_x = [-1 0 1; -2 0 2; -1 0 1];
sobel_y = [-1 -2 -1; 0 0 0; 1 2 1];
Ix = myimfilter(I, sobel_x);
Iy = myimfilter(I, sobel_y);
res = abs(Ix) + abs(Iy);
imshow(res);
function output = myimfilter(image, kernel)
image = im2double(image);
[imageHeight, imageWidth, ~] = size(image);
[kernelHeight, kernelWidth] = size(kernel);
padHeight = floor(kernelHeight / 2);
padWidth = floor(kernelWidth / 2);
paddedImage = padarray(image, [padHeight, padWidth], 'replicate', 'both');
output = zeros(size(image), 'like', image);
kernel = rot90(kernel, 2);
for i = 1:imageHeight
for j = 1:imageWidth
imagePatch = paddedImage(i:i+kernelHeight-1, j:j+kernelWidth-1, :);
for k = 1:size(image, 3)
output(i, j, k) = sum(sum(kernel .* imagePatch(:, :, k)));
end
end
end
end
확실히 uint8로 출력되던 imfilter와 다르게 에지가 잘 검출되었다.
요약
이미지 샤프닝
1. 라플라시안 필터
a. 정의: 원본 이미지에서 이미지를 두 번 미분한 것을 빼서 에지를 강조하는 필터
b. 장점: 세밀한 에지 감지 및 얇은 에지
c. 단점: 노이즈에 민감하며, 이중 에지 효과가 발생할 수 있음
2. Unsharp Masking
a. 정의: 원본 이미지를 블러 처리하여 생성된 흐릿한 이미지와 원본 이미지 사이의 차이를 이용한 필터
b. 장점: 매개변수를 조절해 샤프닝의 정도를 세밀하게 조정할 수 있으며, 노이즈가 제외되도록 할 수 있음
c. 단점: 계산 과정이 복잡하며, 에지 주변에 밝은 테두리가 생기는 할로 현상이 생길 수 있음
3. 일차 미분
a. 정의: 수평과 수직 방향의 밝기 변화율을 측정하여 간단하고 빠른 계산을 보장하는 필터
b. 장점: 간단하고 빠른 계산이 가능하며, 방향성 감지에 용이
c. 단점: 노이즈에 민감하게 반응하고, 에지 두께가 두꺼움
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Fourier Theory (2) (0) | 2023.11.18 |
|---|---|
| [디지털영상처리] Fourier theory (1) (0) | 2023.11.16 |
| [디지털영상처리] Image Sharpening (2) (0) | 2023.11.07 |
| [디지털영상처리] Image Sharpening (1) (0) | 2023.11.06 |
| [디지털영상처리] Smoothing Spatial Filtering (0) | 2023.11.05 |