본문
Zero Padding
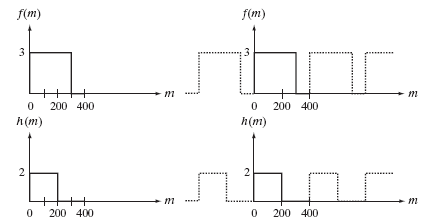
디지털 영상 처리에서 이미지를 주기적인 신호로 간주하고 처리한다. 위의 그래프에서 왼쪽에 있는 것이 원래 신호고, 오른쪽에 있는 그래프가 이미지가 주기적이라는 것을 가정한 상태다. 이는 이미지의 한쪽 끝과 다른 쪽 끝이 서로 연결되어 있다고 가정하는 것과 동일하다. 이러한 처리 방식에서는 이미지의 오른쪽 끝과 왼쪽 끝, 상단과 하단이 서로 감싸는 Wraparound Error가 발생할 수 있다. 즉, 컨볼루션 연산 중 이미지의 한쪽 끝의 값이 반대편 끝에 영향을 미친다. 위의 두 신호 f(m)과 h(m)에 대해 컨볼루션 연산을 적용하는 과정을 통해 왜 이러한 일이 발생하는지 알아보자.

컨볼루션의 정의에 따라 h(m)을 y축에 대해 대칭시키면 다음과 같이 표현할 수 있을 것이다. 여기까지는 큰 문제가 없지만, 해당 신호를 컨볼루션 정의에 따라 h(x-m)으로 평행이동 시키면 다음과 같은 문제가 발생한다.


원래 신호는 왼쪽과 같이 m축으로 x부터 400까지 값이 0이어야 한다. 하지만 이미지가 주기적이라는 가정으로 인해 신호의 끝과 끝이 image frequency 간섭으로 인해 연결되는 현상이 발생한다. 이로 인해 컨볼루션 결과가 왜곡되어 원하지 않는 결과가 나온다.

이러한 간섭 현상을 방지해 주는 게 바로 Zero Padding이다. 이는 이미지 테두리 주변에 0의 값을 갖는 픽셀들을 추가하여 이미지의 가장자리에서 발생할 수 있는 왜곡을 줄이고, 컨볼루션 연산 시 발생하는 경계 효과를 완화한다. 이를 통해 이미지 경계 부분의 데이터 손실을 방지하고, 컨볼루션 결과의 정확도를 높일 수 있다.
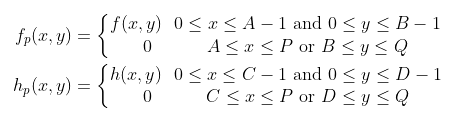
다음과 같이 AxB 사이즈의 원본 이미지 f(x, y), CxD 크기의 필터 이미지 h(x, y)가 있다고 가정해 보자. 여기서 Wraparound Error를 방지하려면 해당 함수에 패딩을 해야 한다. 일반적으로 각 축에 대해 두 이미지의 크기를 더한 값보다 크게 0 픽셀들을 추가하므로, P >= A+C-1, Q >= B+D-1이 된다. 이때 푸리에 변환을 적용하기 위해 행렬 연산을 해야 하므로 f와 h의 크기가 같아진다는 것도 체크해 두자.
Filtering in the Frequency Domain
주파수 영역에서 필터링을 하기 위해선 다음과 같은 절차가 존재한다.
1. 이미지에 Zero Padding을 적용
2. DFT를 적용하고 주파수 영역에서 저주파 대역이 이미지의 중심에 오도록 (-1)^(x+y)를 곱함
3. 실수 대칭 필터 함수 H(u, v)를 설계
- Phase Shift가 발생하지 않게 하며, 공간 도메인에서 실수 값을 가지게 하는 필터가 되게 하기 위함. 즉, 공간 영역에서 컨볼루션이 주파수 영역에서 곱셈인데, 역변환 과정에서 해당 명제가 참이 되려면 필터 함수가 실수값이어야 한다.
4. 필터를 적용
ILPF/IHPF


또한 주파수 영역에서 필터는 크게 이상적인 필터, 버터워스 필터, 가우시안 필터가 존재한다. 필터를 적용하기 위해 픽셀값 (u, v)로부터 떨어진 거리 D(u, v)를 알아야 하는데, 이 값을 위와 같이 정의한다.


주파수 영역에서 자주 사용되는 필터는 크게 세 가지다. 그중 하나는 Ideal Filter로, 이상적인 필터다. 이는 매우 단순하면서도 직관적인 방법으로 동작한다. 즉, 임계값 이하의 주파수 성분만 통과시키고, 그 이상의 성분은 차단시킨다. 위에 나타난 수식은 ILPF지만, IHPF를 설계하고 싶으면 D(u, v) >= D0로 설정하면 된다.

하지만 이상적인 필터는 그 급격한 전이 특성 때문에 몇 가지 문제를 야기할 수 있다. 특히, 이상적 필터는 주파수 영역에서 날카로운 경계를 가지고 있어, 빈도가 0에서 D0까지 갑자기 떨어진다. 이러한 급격한 변화는 원하지 않는 링잉 효과(Ringing Effect)를 발생시킬 수 있다. 링잉 효과는 이미지에 부자연스러운 진동성 무늬나 고리 모양의 아티팩트를 만들어내며, 이는 필터가 적용되는 부분에서 많은 주기 함수들이 겹치면서 생기는 현상이다.
BLPF/BHPF
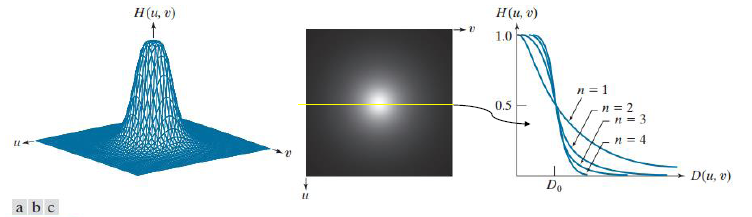
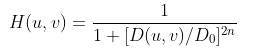
다음은 중심에서 멀어질수록 그 값이 0으로 접근하는 특성을 갖는 버터워스(Butterworth) 필터다. 해당 필터는 이상적인 필터와 달리 부드러운 전이 특성을 갖고 있어, 링잉 효과를 크게 줄일 수 있다. 위에 기재된 수식은 저역 통과 필터지만, 해당 수식에서 1을 빼면 고역 통과 필터를 구현할 수 있다.
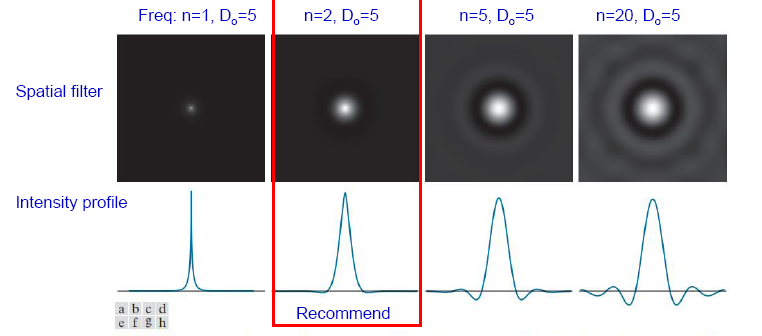
하지만 n의 값이 증가함에 따라 필터의 전이 대역이 더욱 날카로워져 링잉 효과가 여전히 존재할 수 있다는 단점이 있다.
GLPF/GHPF
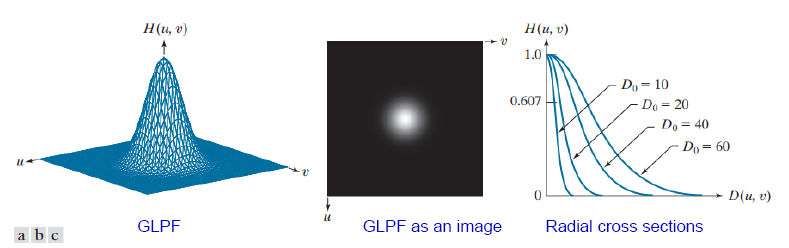
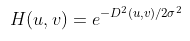
마지막으로 평균과 표준편차를 이용하는 가우시안(Gaussian) 필터다. 이 필터는 자연스러운 부드러움과 함께 노이즈를 효과적으로 감소시키는 특징을 갖고 있다. 해당 수식을 통해 중심점에서 멀어질수록 주파수 영역에서의 특정 점 (u, v)가 감소하며, 시그마의 값에 따라 필터의 폭이 결정된다. 즉, 표준편차가 클수록 필터는 더 넓은 범위의 주파수를 포함하게 되어 이미지가 더욱 부드럽게 처리된다. 이로 인해 링잉 효과가 완전히 제거된다.
필터 구현
function res = myFilter(I, filterType, D0)
F = fftshift(fft2(double(I)));
[u, v] = size(I);
H = zeros(u, v);
for i = 1:v
for j = 1:u
D = sqrt((i - u/2)^2 + (j - v/2)^2);
switch filterType
case 'ILPF'
if D < D0
H(i,j) = 1;
end
case 'IHPF'
if D >= D0
H(i,j) = 1;
end
case 'BLPF'
H(i,j) = 1 / (1 + (D / D0)^(4));
case 'BHPF'
H(i, j) = 1 - (1/(1 + (D / D0)^(4)));
case 'GLPF'
H(i,j) = exp(-(D^2) / (2 * D0^2));
case 'GHPF'
H(i,j) = 1 - exp(-(D^2) / (2 * D0^2));
otherwise
error('잘못된 필터 이름입니다.');
end
end
end
F_filtered = F .* H;
res = uint8(ifft2(ifftshift(F_filtered)));
end다음은 위에서 언급한 필터를 간단하게 구현한 코드다. 입력 이미지를 받아온 후 크기를 동일하게 맞추고 D0값을 설정해 준 후 해당 함수를 사용하면 원하는 결과가 나온다.
요약
주파수 영역에서의 필터링
1. 전제
a. Nyquist-Shannon 샘플링 정리 만족: 샘플링 속도는 신호의 최대 주파수의 두 배 이상(에일리어싱 방지)
b. 이미지의 범위를 무한대로 넓혔을 때 주기성을 갖는다고 가정
2. 과정
a. 이미지에 Zero Padding(0을 추가하는 작업)을 적용
b. DFT를 적용하고 주파수 영역에서 저주파 대역이 이미지의 중심에 오도록 (-1)^(x+y)를 곱함
c. 실수 대칭 필터 함수 H(u, v)를 설계
- Phase Shift가 발생하지 않고, 공간 도메인에서 실수 값을 가지게 하는 필터가 되게 하기 위함
3. 종류: Ideal, Butterworth, Gaussian
- Ideal, Butterworth는 Ringing 효과(진동되는 것처럼 울리는 현상)가 존재함
'CS > 디지털영상처리' 카테고리의 다른 글
| [디지털영상처리] Color Image Processing (2) (2) | 2024.01.24 |
|---|---|
| [디지털영상처리] Color Image Processing (1) (2) | 2024.01.23 |
| [디지털영상처리] Filtering in Frequency Domain (2) (2) | 2024.01.04 |
| [디지털영상처리] Filtering in Frequency Domain (1) (2) | 2023.12.07 |
| [디지털영상처리] Fourier Theory (2) (0) | 2023.11.18 |