<본 카테고리는 "코딩 테스트를 위한 자료 구조와 알고리즘 with C++을 기반으로 작성하였습니다>
벨만-포드 알고리즘
개요
이전 게시물들에서는 그래프 내의 두 정점 사이의 최단 경로를 찾는 방법들에 대해 다루었다. 특히 가중치가 부여된 그래프에서 최단 경로를 찾는 대표적인 방법인 다익스트라 알고리즘은 그리디 알고리즘의 원리를 활용해 각 단계에서 최단 경로를 계산한다. 이 방법은 효율성 면에서 뛰어나지만, 한 가지 큰 제약 사항이 존재하는데, 바로 음의 가중치를 가진 에지를 처리할 수 없다는 점이다. 다익스트라 알고리즘이 음의 가중치를 처리하지 못하는 이유는 그 알고리즘의 핵심 원리에 있다. 이 알고리즘은 '현재까지 발견된 최단 경로'를 기반으로 작동한다. 그리고 이 경로는 더 이상 개선될 수 없다고 가정한다. 즉, 한 번 '최단'으로 판단된 경로는 그 이후에 변경되지 않는다.
하지만 음의 가중치가 그래프에 포함되면 이러한 가정이 무너진다. 예를 들어, 어떤 경로가 '현재까지의 최단 경로'로 선택된 후에 이어지는 에지의 가중치가 음수라면, 그 경로의 전체 비용이 더 작아질 수 있다. 이는 이미 '최단'으로 판정된 경로를 다시 조정해야 함을 의미하고, 이는 다익스트라 알고리즘이 가정하는 바와 모순된다. 이 때문에 다익스트라 알고리즘은 음의 가중치를 가진 그래프에서는 정확한 결과를 도출하지 못한다.

예를 들어, 다음과 같은 그래프를 다익스트라 알고리즘을 이용하여 최단 경로를 구한다고 가정해 보자. 알고리즘은 A에서 B로 이동하고, 가중치가 5인 에지를 통해 B에서 C로 이동한다. 그다음에는 C에서 D로 이동한다.
그러나 실제로는 B에서 D로 이동한 후, D에서 C로 되돌아가는 경로가 최단 거리를 가진다. B에서 C로 직접 가는 경우 가중치는 5이지만, B에서 D를 거려 C로 가는 경우 총 가중치 10 + (-7) = 3으로 더 짧다. 이러한 상황은 다익스트라 알고리즘이 음의 가중치를 올바르게 처리하지 못하기 때문에 발생한다. 따라서 이러한 한계를 극복할 수 있는 알고리즘의 필요성이 대두된다.
본문
음의 가중치를 가진 그래프를 다루는 경우, 벨만-포드 알고리즘(bellman-ford algorithm)을 사용할 수 있다. 이 알고리즘은 그래프의 모든 에지를 (V-1) 번, 즉 정점 수-1 만큼 반복적으로 검토하여 점진적으로 최단 거리를 결정한다. 이는 다익스트라의 그리디 선택 방식과는 다르게, 그래프의 모든 경로를 고려한다. 비록 벨만-포드 알고리즘은 다익스트라 알고리즘에 비해 상대적으로 높은 시간 복잡도를 가지지만, 음의 가중치를 포함하는 모든 유형의 그래프에 대해 정확한 최단 경로를 찾을 수 있다는 큰 장점이 있다.
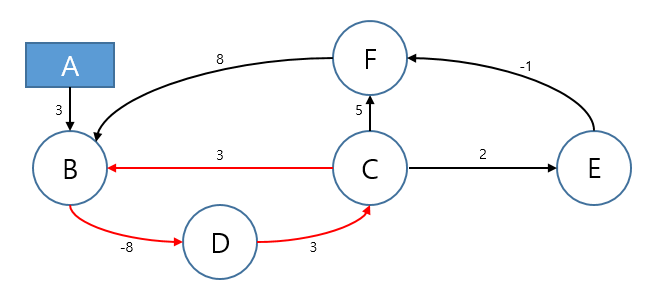
다음과 같은 그래프가 있다고 가정해 보자. 여기서 최단 경로를 계산하다 보면 A → B → D → C → B로 이어지는 경로에서 총가중치가 음수가 된다. 이를 음수 가중치 사이클(negative weight cycle)이라고 하는데, 이 존재는 이 그래프에서 최단 경로를 찾는 것을 불가능하게 만든다. 이 사이클을 거칠 때마다 총가중치가 감소하기 때문에, 무한히 많이 사이클을 돌면 무한히 가중치가 감소하게 된다. 즉, 이런 그래프에서는 최단 경로라는 개념이 실질적으로 의미가 없게 된다. 벨만-포드 알고리즘은 이러한 음의 사이클의 존재 여부를 탐지할 수 있으므로, 해당 사이클이 반복적으로 계산에 사용되어 최종 결과가 왜곡될 수 있는 것을 방지한다.
구현
#include <vector>
#include <iostream>
struct edge
{
int _src, _dst, _weight;
};다음과 같이 에지를 표현할 구제체 edge를 정의한다. 이는 출발 정점의 ID, 목적 정점의 ID, 가중치를 저장한다.
std::vector<int> bellman_ford(std::vector<edge> edges, int v, int start)
{
std::vector<int> distance(v, INT_MAX);
distance[start] = 0;
for (int i = 0; i < v - 1; ++i)
{
for (const auto& e : edges)
{
if (distance[e._src] == INT_MAX)
continue;
if (distance[e._dst] > distance[e._src] + e._weight)
distance[e._dst] = distance[e._src] + e._weight;
}
}벨만-포드 알고리즘을 구현한 bellman_ford() 함수다. 이 함수는 그래프를 표현하는 에지 리스트와 정점의 개수, 출발 정점 번호를 인자로 받고, 거리 값 배열을 반환한다. 이 함수 내부에서는 v개 크기의 거리 값 배열을 사용하고, 이 배열의 초깃값을 INT_MAX로 지정한다.
그리고 V - 1번까지의 루프를 설정하여, 각각의 반복마다 모든 에지를 검토하고 각 정점까지의 거리 값을 업데이트한다. 이 과정에서 만약 시작 정점까지의 거리가 INT_MAX라면, 이는 해당 정점까지 도달 가능한 경로가 아직 발견되지 않았음을 의미하므로, 이에 대한 계산은 스킵한다. 이러한 처리는 불필요한 계산을 방지하고 알고리즘의 효율성을 높이는 데 도움이 된다. 만약 시작 정점에서 목적지 정점까지의 현재 거리 값보다 (시작 정점에서 에지 출발점까지의 거리 값 + 에지 가중치)가 더 작다면, 목적지 정점까지의 거리 값을 교체한다.
for (const auto& e : edges)
{
if (distance[e._src] == INT_MAX)
continue;
if (distance[e._dst] > distance[e._src] + e._weight)
{
std::cerr << "negative weight cycle occurrence\n";
return {};
}
}
return distance;
}음수 가중치 사이클을 검사하는 부분이다. 최단 경로를 구한 후에 한 번 더 각 에지를 검사하여 시작 정점에서 목적지 정점까지의 현재 거리 값이 (시작 정점에서 에지 출발점까지의 거리 값 + 에지 가중치) 보다 큰지 확인한다. 만약, 이것이 참이라면, 음수 가중치 사이클이 존재한다고 판단할 수 있다. 이는 우리가 이미 최단 거리를 찾았다고 가정하고 있기 때문에, 더 짧은 경로가 발견되면 이는 음수 가중치 사이클에서 기인하기 때문이다.
void run(std::vector<edge> edges, int v)
{
std::vector<int> distance = bellman_ford(edges, v, 0);
if (!distance.empty())
{
std::cout << "[Minimum distance from vertex 0]\n";
for (int i = 0; i < distance.size(); ++i)
{
if (distance[i] == INT_MAX)
std::cout << "vertex[" << i << "]: not visiting\n";
else
std::cout << "vertex[" << i << "]: " << distance[i] << "\n";
}
}
}마지막으로 그래프와 정점의 개수를 넣어 각 정점의 최단 거리 값 배열을 출력하는 함수 run()을 작성하였다.
int main()
{
int v = 6;
std::vector<edge> edges;
std::vector<std::vector<int>> edge_map
{
{0, 1, 3},
{1, 3, -8},
{2, 1, 3},
{2, 5, 5},
{3, 2, 3},
{2, 4, 2},
{4, 5, -1},
{5, 1, 8}
};
for (const auto& e : edge_map)
edges.push_back(edge{ e[0], e[1], e[2] });
run(edges, 6);
edges.clear(); std::cout << "\n";
edge_map =
{
{0, 1, 3},
{1, 2, 5},
{1, 3, 10},
{3, 2, -7},
{2, 4, 2}
};
for (const auto& e : edge_map)
edges.push_back(edge{ e[0], e[1], e[2] });
run(edges, 5);
}
총합본
#include <vector>
#include <iostream>
struct edge
{
int _src, _dst, _weight;
};
std::vector<int> bellman_ford(std::vector<edge> edges, int v, int start)
{
std::vector<int> distance(v, INT_MAX);
distance[start] = 0;
for (int i = 0; i < v - 1; ++i)
{
for (const auto& e : edges)
{
if (distance[e._src] == INT_MAX)
continue;
if (distance[e._dst] > distance[e._src] + e._weight)
distance[e._dst] = distance[e._src] + e._weight;
}
}
for (const auto& e : edges)
{
if (distance[e._src] == INT_MAX)
continue;
if (distance[e._dst] > distance[e._src] + e._weight)
{
std::cerr << "negative weight cycle occurrence\n";
return {};
}
}
return distance;
}
void run(std::vector<edge> edges, int v)
{
std::vector<int> distance = bellman_ford(edges, v, 0);
if (!distance.empty())
{
std::cout << "[Minimum distance from vertex 0]\n";
for (int i = 0; i < distance.size(); ++i)
{
if (distance[i] == INT_MAX)
std::cout << "vertex[" << i << "]: not visiting\n";
else
std::cout << "vertex[" << i << "]: " << distance[i] << "\n";
}
}
}
int main()
{
int v = 6;
std::vector<edge> edges;
std::vector<std::vector<int>> edge_map
{
{0, 1, 3},
{1, 3, -8},
{2, 1, 3},
{2, 5, 5},
{3, 2, 3},
{2, 4, 2},
{4, 5, -1},
{5, 1, 8}
};
for (const auto& e : edge_map)
edges.push_back(edge{ e[0], e[1], e[2] });
run(edges, 6);
edges.clear(); std::cout << "\n";
edge_map =
{
{0, 1, 3},
{1, 2, 5},
{1, 3, 10},
{3, 2, -7},
{2, 4, 2}
};
for (const auto& e : edge_map)
edges.push_back(edge{ e[0], e[1], e[2] });
run(edges, 5);
}요약
벨만-포드 알고리즘
1. 정의: 음수 가중치를 포함한 최단 경로 탐색 알고리즘
2. 특징
- 음수 가중치를 고려
- 다익스트라 알고리즘이 잘못 해석할 수 있는 그래프에 대해서도 정확한 결과를 제공
- 음수 가중치 사이클을 찾을 수 있음
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 다익스트라 최단 경로 알고리즘 (0) | 2023.06.17 |
|---|---|
| [알고리즘] 프림 알고리즘 (0) | 2023.06.15 |
| [알고리즘] 그래프 순회 문제 (0) | 2023.06.14 |
| [알고리즘] 그리디 알고리즘 - 그래프 컬러링 (0) | 2023.05.30 |
| [알고리즘] 그리디 알고리즘 - 최소 신장 트리 문제 (2) (0) | 2023.05.29 |