<본 카테고리는 "코딩 테스트를 위한 자료 구조와 알고리즘 with C++을 기반으로 작성하였습니다>
프림의 최소 신장 트리 알고리즘
프림 알고리즘
프림 알고리즘(Prim's Algorithm)은 최소 신장 트리 문제를 해결하는 그리디 알고리즘 중 하나다. 그래프의 임의의 정점에서 시작하여, 그래프의 모든 정점을 포함하고 모든 간선의 가중치 합이 최소인 트리를 찾는 알고리즘으로서, BFS의 동작 방식과 유사하다. 동작 과정은 다음과 같다.
- 시작 노드를 선택하고, 선택한 정점을 트리에 추가
- 선택한 노드에 인접하고 트리에 연결되지 않은 노드로 연결된 간선들 중, 가장 작은 가중치를 가진 간선을 추가
- 그래프의 모든 노드가 트리에 추가될 때까지 반복
예시
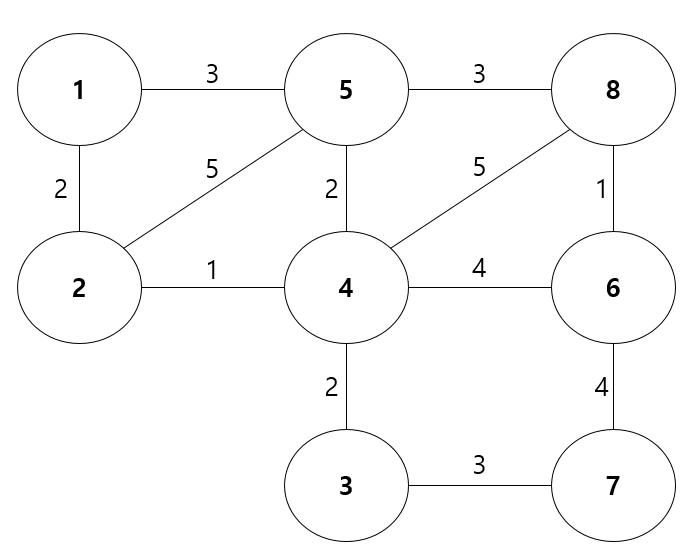
다음과 같은 그래프가 있다고 가정하고, 이러한 그래프에 프림 알고리즘을 적용하여 최소 신장 트리를 구하는 과정을 살펴보자.

먼저 시작 정점을 제외하고, 모든 정점의 거리 값을 무한대로 초기화한다. 이는 그래프의 시작 정점을 제외하고 모든 정점들이 MST에 포함되지 않았음을 나타내기 위해서다. 이를 통해 최소 신장 트리에 아직 포함되지 않은 정점들은 다른 어떤 정점보다 거리가 멀다고 판단되어, 그 정점들이 먼저 선택되지 않도록 한다.
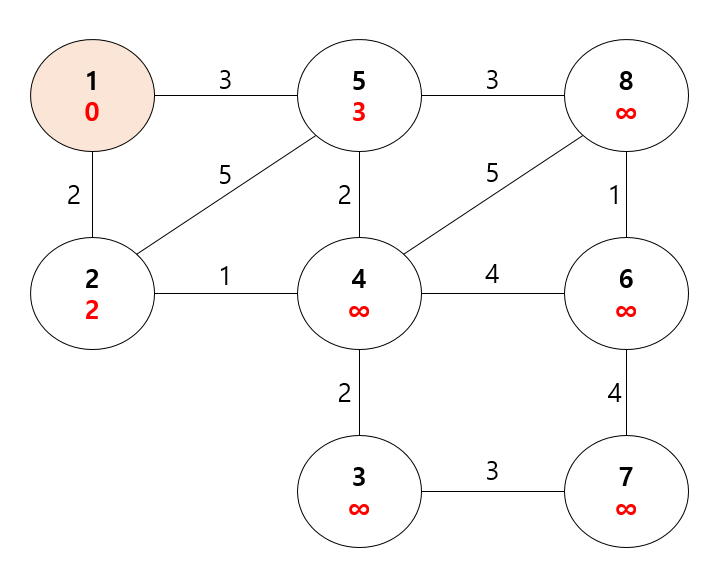
먼저 정점을 하나 선택한다. 이 정점 U와 인접한 모든 정점 V에 대해, 만약 V의 거리 값이 (U,V)의 에지 가중치보다 크면 V의 거리 값을 (U,V)의 에지 가중치로 설정한다.
여기서 정점1과 정점5 사이의 거리는 3이다. 따라서 정점5의 현재 거리 값인 ∞이 현재 거리 값인 3보다 크므로, 정점5의 거리 값을 3으로 업데이트하였다. 또한, 정점1과 정점2 사이의 거리는 2고, 정점2의 현재 거리 값은 ∞이므로, 정점2의 거리 값을 2로 업데이트하였다.

위와 같은 방법으로 모든 정점에 안착하면, 다음과 같이 최종 MST가 완성된다.
구현
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <queue>
#include <limits>
using us = unsigned;
template <typename T>
struct edge
{
us _src, _dst;
T _weight;
};
template <class T>
class graph
{
us _v;
std::vector<edge<T>> _edges;
public:
graph(us n) : _v(n)
{
}
auto vertices() const
{
return _v;
}
auto& edges() const
{
return _edges;
}
auto edges(us v) const
{
std::vector<edge<T>> edges_from_v;
for (const auto& e : _edges)
{
if (e._src == v)
edges_from_v.push_back(e);
}
return edges_from_v;
}
void add_edge(edge<T>&& e)
{
if (e._src >= 1 && e._src <= _v && e._dst >= 1 && e._src <= _v)
_edges.push_back(e);
else
std::cerr << "error: invalid range\n";
}
template <typename t>
friend std::ostream& operator << (std::ostream& os, const graph<t>& g)
{
for (us i = 1; i < g.vertices(); ++i)
{
os << i << ":\t";
auto edges = g.edges(i);
for (const auto& e : edges)
os << "{" << e._dst << ": " << e._weight << "}, ";
os << "\n";
}
return os;
}
};
template <typename T>
struct label
{
us _ID;
T _distance;
inline bool operator > (const label<T>& l) const
{
return this->_distance > l._distance;
}
};에지 구조체와 그래프 클래스, 그리고 라벨 구조체를 초기화한다.
template <typename T>
auto prim(const graph<T>& g, us src)
{
std::priority_queue<label<T>, std::vector<label<T>>, std::greater<label<T>>> pq;
std::vector<T> distance(g.vertices(), std::numeric_limits<T>::max());
std::set<us> visited;
std::vector<us> mst;
pq.push(label<T>{src, 0});
while (!pq.empty())
{
auto current = pq.top();
pq.pop();
if (visited.find(current._ID) == visited.end())
{
mst.push_back(current._ID);
for (const auto& e : g.edges(current._ID))
{
auto neighbor = e._dst;
auto new_distance = e._weight;
if (new_distance < distance[neighbor])
{
pq.push(label<T>{neighbor, new_distance});
distance[neighbor] = new_distance;
}
}
visited.insert(current._ID);
}
}
return mst;
}프림 알고리즘을 구현한 prim() 함수다. 최소 힙 pq, 모든 정점에서 거리를 최대로 설정한 distance, 방문한 정점 visited, 최소 신장 트리 mst를 초기화한다. 이때 거리는 무한대로 초기화해야하므로, 주어진 자료형 T로 표현 가능한 최대값을 반환하기 위해 std::numeric_limits<T>::max()를 사용하였다.
현재 정점을 이전에 방문하지 않았다면, 최소 신장 트리에 정점을 넣는다. 그리고 인접한 정점의 거리 값이 새로운 경로에 의한 거리 값보다 크면 힙에 추가하고, 거리 값을 업데이트 하는 방식으로 구현하였다.
int main()
{
graph<us> g(9);
std::map<us, std::vector<std::pair<us, us>>> edge_map;
edge_map[1] = { {2, 2}, {5, 3} };
edge_map[2] = { {1, 2}, {5, 5}, {4, 1} };
edge_map[3] = { {4, 2}, {7, 3} };
edge_map[4] = { {2, 1}, {3, 2}, {5, 2}, {6, 4}, {8, 5} };
edge_map[5] = { {1, 3}, {2, 5}, {4, 2}, {8, 3} };
edge_map[6] = { {4, 4}, {7, 4}, {8, 1} };
edge_map[7] = { {3, 3}, {6, 4} };
edge_map[8] = { {4, 5}, {5, 3}, {6, 1} };
for (const auto& i : edge_map)
{
for (const auto& j : i.second)
g.add_edge(edge<us> {i.first, j.first, j.second});
}
std::cout << "[Input]\n";
std::cout << g << "\n";
auto mst = prim<us>(g, 1);
std::cout << "[MST]\n";
for (const auto& val : mst)
std::cout << val << "\n";
std::cout << "\n";
}
총합본
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <queue>
#include <limits>
using us = unsigned;
template <typename T>
struct edge
{
us _src, _dst;
T _weight;
};
template <class T>
class graph
{
us _v;
std::vector<edge<T>> _edges;
public:
graph(us n) : _v(n)
{
}
auto vertices() const
{
return _v;
}
auto& edges() const
{
return _edges;
}
auto edges(us v) const
{
std::vector<edge<T>> edges_from_v;
for (const auto& e : _edges)
{
if (e._src == v)
edges_from_v.push_back(e);
}
return edges_from_v;
}
void add_edge(edge<T>&& e)
{
if (e._src >= 1 && e._src <= _v && e._dst >= 1 && e._src <= _v)
_edges.push_back(e);
else
std::cerr << "error: invalid range\n";
}
template <typename t>
friend std::ostream& operator << (std::ostream& os, const graph<t>& g)
{
for (us i = 1; i < g.vertices(); ++i)
{
os << i << ":\t";
auto edges = g.edges(i);
for (const auto& e : edges)
os << "{" << e._dst << ": " << e._weight << "}, ";
os << "\n";
}
return os;
}
};
template <typename T>
struct label
{
us _ID;
T _distance;
inline bool operator > (const label<T>& l) const
{
return this->_distance > l._distance;
}
};
template <typename T>
auto prim(const graph<T>& g, us src)
{
std::priority_queue<label<T>, std::vector<label<T>>, std::greater<label<T>>> pq;
std::vector<T> distance(g.vertices(), std::numeric_limits<T>::max());
std::set<us> visited;
std::vector<us> mst;
pq.push(label<T>{src, 0});
while (!pq.empty())
{
auto current = pq.top();
pq.pop();
if (visited.find(current._ID) == visited.end())
{
mst.push_back(current._ID);
for (const auto& e : g.edges(current._ID))
{
auto neighbor = e._dst;
auto new_distance = e._weight;
if (new_distance < distance[neighbor])
{
pq.push(label<T>{neighbor, new_distance});
distance[neighbor] = new_distance;
}
}
visited.insert(current._ID);
}
}
return mst;
}
int main()
{
graph<us> g(9);
std::map<us, std::vector<std::pair<us, us>>> edge_map;
edge_map[1] = { {2, 2}, {5, 3} };
edge_map[2] = { {1, 2}, {5, 5}, {4, 1} };
edge_map[3] = { {4, 2}, {7, 3} };
edge_map[4] = { {2, 1}, {3, 2}, {5, 2}, {6, 4}, {8, 5} };
edge_map[5] = { {1, 3}, {2, 5}, {4, 2}, {8, 3} };
edge_map[6] = { {4, 4}, {7, 4}, {8, 1} };
edge_map[7] = { {3, 3}, {6, 4} };
edge_map[8] = { {4, 5}, {5, 3}, {6, 1} };
for (const auto& i : edge_map)
{
for (const auto& j : i.second)
g.add_edge(edge<us> {i.first, j.first, j.second});
}
std::cout << "[Input]\n";
std::cout << g << "\n";
auto mst = prim<us>(g, 1);
std::cout << "[MST]\n";
for (const auto& val : mst)
std::cout << val << "\n";
std::cout << "\n";
}요약
프림 알고리즘
1. 정의: 경계를 관통하는 에지 중 가장 가중치가 작은 에지를 선택하고, 이 에지에 연결된 정점을 방문하는 최소 신장 트리 알고리즘
2. 과정
a. 시작 노드를 선택하고 트리에 추가
b. 인접한 모든 정점에 대해 거리 값과 에지 가중치를 비교
c. 정점의 거리 값이 에지 가중치보다 크면, 거리 값을 에지 가중치로 설정
3. 특징
- 시간 복잡도가 O(E logV), 만약 피보나치 최소 힙 구조를 사용하면 O(E + VlogV)로 향상
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 벨만-포드 알고리즘 (0) | 2023.06.23 |
|---|---|
| [알고리즘] 다익스트라 최단 경로 알고리즘 (0) | 2023.06.17 |
| [알고리즘] 그래프 순회 문제 (0) | 2023.06.14 |
| [알고리즘] 그리디 알고리즘 - 그래프 컬러링 (0) | 2023.05.30 |
| [알고리즘] 그리디 알고리즘 - 최소 신장 트리 문제 (2) (0) | 2023.05.29 |