<본 카테고리는 "코딩 테스트를 위한 자료 구조와 알고리즘 with C++을 기반으로 작성하였습니다>
분할 정복
개요
분할 정복(divide-and-conquer)은 복잡하고 해결하기 어려운 문제를 작은 부분 문제로 나눠서 해결하는 방법론이다. 이 접근법의 핵심은 큰 문제를 둘 이상의 하위 문제로 분할하고, 이러한 각각의 하위 문제를 독립적으로 해결한 후, 그 결과를 결합하여 원래 문제의 해법을 도출하는 것이다. 이 기법은 복잡한 문제를 간소화함으로써 알고리즘의 효율성을 증대시키는 데에 중요한 역할을 한다.
주어진 문제를 분할 정복 방식으로 해결하려면 다음과 같은 세 단계가 필요하다.
- 분할(divide): 주어진 문제를 동일한 방식으로 해결할 수 있는 여러 서브 문제로 나눔
- 정복(conquer): 각 서브 문제에 대한 해답을 구함
- 결합(combine): 각 서브 문제의 해답을 결합하여 전체 문제에 대한 해답을 구함
이러한 단계를 거치는 분할 정복 알고리즘은 문제의 규모를 줄이고 재귀적인 구조를 형성함으로써 코드를 간결하게 만드는 특성이 있다. 또한, 부분 문제는 독립적으로 해결 가능하므로 병렬 처리에 적합하다. 하지만 재귀 호출에 대한 오버헤드가 존재할 수 있으며, 추가적인 메모리를 필요로 할 수 있다. 또한, 문제의 해결책을 어떻게 결합하는지에 따라 알고리즘의 성능이 크게 달라질 수 있다.
정렬
정렬 알고리즘 구현의 주요 고려사항을 살펴보자.
- 모든 데이터 타입에 대해 동작
- 컴퓨터의 메인 메모리보다 큰 용량의 데이터에 대해서도 동작
- 점근전 시간 복잡도 측면이나 실제 동작 시에 빠르게 동작
나열된 세 가지 조건을 모두 만족하면 좋겠지만, 현실적으로 2번과 3번 조건을 동시에 만족하기는 어렵다. 특히, 컴퓨터의 주 메모리 용량을 초과하는 데이터를 처리하는 경우에 추가적인 전략이 필요하다. 추후에 다루겠지만, 전체 데이터의 일부만을 메모리에 올려놓고 동작하는 방식, 즉 외부(external) 정렬 방식을 고려해 볼 수 있겠다.
병합 정렬
대규묘 데이터를 정렬에 이상적인 병합(merge) 정렬은 전체 집합을 작은 크기의 부분집합으로 분할하여 각각을 정렬하고, 이를 오름차순 또는 내림차순으로 합치는 알고리즘이다. 예를 들어 벡터에 {2, 6, 7, 3, 1, 9, 5, 4, 8}이라는 원소가 있고, 이를 병합 정렬 방식으로 처리한다고 가정해 보자.
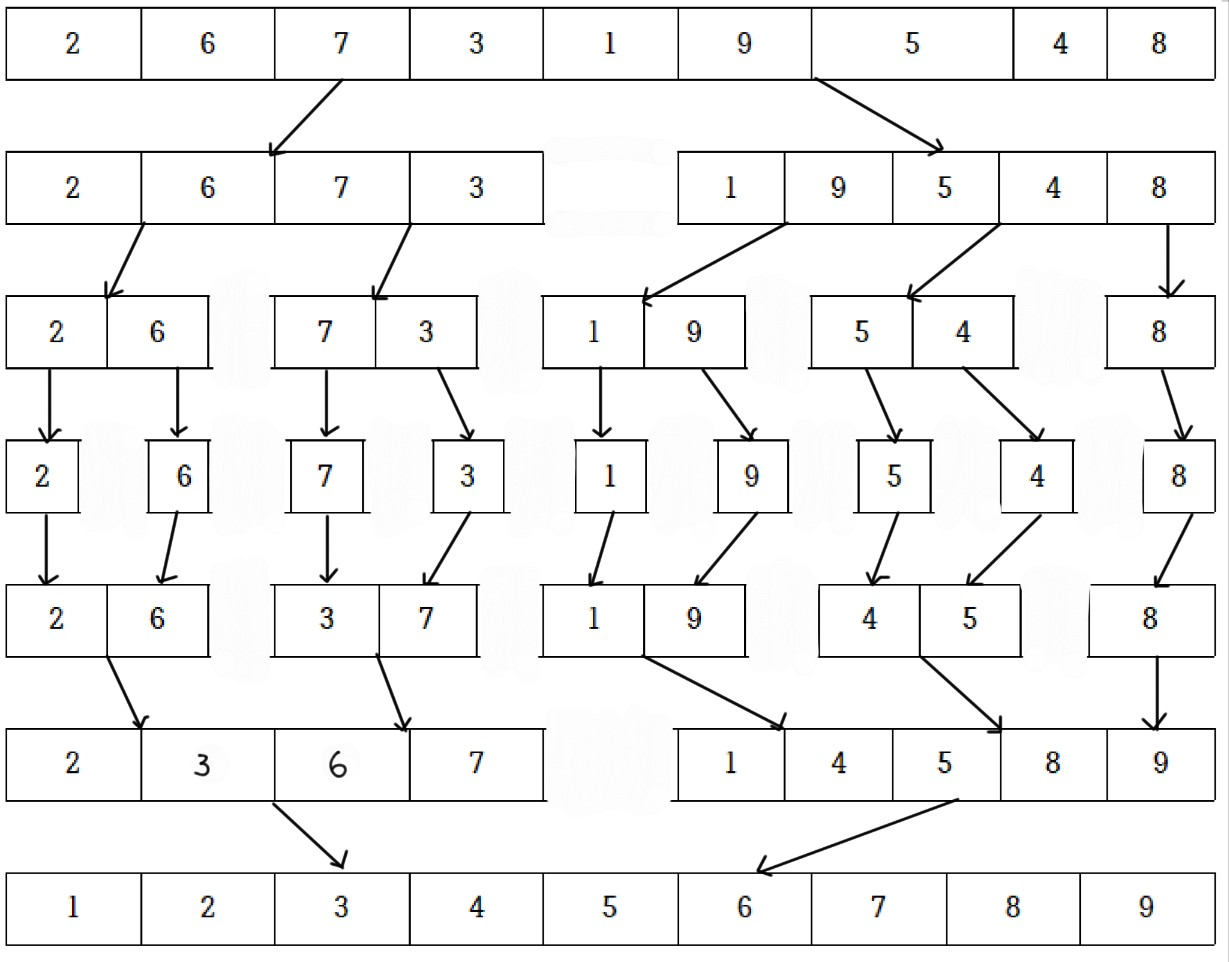
초기 배열 {2, 6, 7, 3, 1, 9, 5, 4, 8}이 각 부분 배열이 하나의 원소만을 포함할 때까지 분할된다. 이후, 배열을 다시 합치는 작업을 반복하되, 병합 과정에서 오름차순 순서가 유지되도록 배열의 원소를 조정한다.
구현
먼저 병합 정렬부터 구현해 보자.
#include <iostream>
#include <vector>
template <typename T>
std::vector<T> merge_sort(std::vector<T> v)
{
if (v.size() > 1)
{
auto mid = size_t(v.size() / 2);
auto left = merge_sort<T>(std::vector<T>(v.begin(), v.begin() + mid));
auto right = merge_sort<T>(std::vector<T>(v.begin() + mid, v.end()));
return merge<T>(left, right);
}
return v;
}앞서 살펴본 것처럼 병합 정렬은 서브 배열이 원소를 하나를 가질 때까지 반틈씩 나누는 과정을 반복한다. 따라서 중앙 크기인 mid를 기준으로 왼쪽과 오른쪽을 나눠 재귀 호출을 한다.
template <typename T>
std::vector<T> merge(std::vector<T>& v1, std::vector<T>& v2)
{
std::vector<T> tmp;
auto it1 = v1.begin();
auto it2 = v2.begin();두 개의 벡터를 병합하는 merge() 함수다. 먼저 합쳐질 결과를 담은 빈 벡터 tmp와 각 벡터의 시작점을 가리키는 반복자 it1, it2를 초기화한다.
while (it1 != v1.end() && it2 != v2.end())
{
if (*it1 < *it2)
{
tmp.emplace_back(*it1);
it1++;
}
else
{
tmp.emplace_back(*it2);
it2++;
}
}병합 절렬의 병합 단계에서는 두 개의 정렬된 배열을 하나의 배열로 합치는 작업을 수행한다. 이 작업을 위해 두 배열의 첫 번째 원소를 비교하고, 더 작은 원소를 결과 배열에 추가한 후, 해당 원소를 가리키는 반복자를 전진시킨다. 이 과정이 필요한 이유는 다음과 같다.
- 두 배열의 첫 번째 원소 중 더 작은 원소는 합쳐진 결과 벡터에서도 앞에 위치
- 두 벡터의 모든 원소를 순차적으로 검토할 수 있음
if (it1 != v1.end())
{
for (; it1 != v1.end(); ++it1)
tmp.emplace_back(*it1);
}
else
{
for (; it2 != v2.end(); ++it2)
tmp.emplace_back(*it2);
}
return tmp;
}두 벡터 중 하나가 끝에 도달했을 때, 아직 순회하지 않은 벡터의 나머지 요소를 모두 tmp 벡터에 추가하여 이를 반환한다.
int main()
{
std::vector<int> v{ 45, 1, 3, 1, 2, 3, 45, 5, 1 ,2 , 44 ,5, 7 };
std::cout << "정렬 전: ";
for (const auto& val : v)
std::cout << val << ' ';
std::cout << std::endl;
v = merge_sort(v);
std::cout << "정렬 후: ";
for (const auto& val : v)
std::cout << val << ' ';
std::cout << std::endl;
}
올바르게 출력되는 것을 확인할 수 있다.
총합본
#include <iostream>
#include <vector>
template <typename T>
std::vector<T> merge(std::vector<T>& v1, std::vector<T>& v2)
{
std::vector<T> tmp;
auto it1 = v1.begin();
auto it2 = v2.begin();
while (it1 != v1.end() && it2 != v2.end())
{
if (*it1 < *it2)
{
tmp.emplace_back(*it1);
it1++;
}
else
{
tmp.emplace_back(*it2);
it2++;
}
}
if (it1 != v1.end())
{
for (; it1 != v1.end(); ++it1)
tmp.emplace_back(*it1);
}
else
{
for (; it2 != v2.end(); ++it2)
tmp.emplace_back(*it2);
}
return tmp;
}
template <typename T>
std::vector<T> merge_sort(std::vector<T> v)
{
if (v.size() > 1)
{
auto mid = size_t(v.size() / 2);
auto left = merge_sort<T>(std::vector<T>(v.begin(), v.begin() + mid));
auto right = merge_sort<T>(std::vector<T>(v.begin() + mid, v.end()));
return merge<T>(left, right);
}
return v;
}
int main()
{
std::vector<int> v{ 2, 6, 7, 3, 1, 9, 5, 4, 8 };
std::cout << "정렬 전: ";
for (const auto& val : v)
std::cout << val << ' ';
std::cout << std::endl;
v = merge_sort(v);
std::cout << "정렬 후: ";
for (const auto& val : v)
std::cout << val << ' ';
std::cout << std::endl;
}
요약
분할 정복
1. 정의: 큰 문제를 분할하여 독립적으로 해결한 후, 결합하는 알고리즘
2. 특징
a. 재귀적 구조
b. 간결성
c. 효율성
d. 병렬 처리
3. 단점
a. 재귀 호출 시 오버헤드 발생
b. 추가적인 메모리 사용
c. 결합에 따른 알고리즘 성능 변화
병합 정렬
1. 정의: 전체 집합을 작은 부분 집합으로 나누어 정렬하는 방식
2. 특징
a. 대규모 데이터 처리에 적합
b. 안정적인 정렬 (O(Nlog(N)) 보장)
c. 병렬 처리
3. 단점
a. 추가적인 메모리 사용
b. 재귀 호출에 따른 오버헤드 및 캐시 효율성 감소
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘 - 개요 및 최단 작업 우선 스케줄링 (0) | 2023.05.22 |
|---|---|
| [알고리즘] 분할 정복 - 맵리듀스 (0) | 2023.05.20 |
| [알고리즘] 분할 정복 - 선형 시간 선택 (2) | 2023.05.19 |
| [알고리즘] 분할 정복 - 퀵 정렬 (0) | 2023.05.16 |
| [알고리즘] 알고리즘 개요 및 이진 탐색 (0) | 2023.05.09 |