<본 카테고리는 "코딩 테스트를 위한 자료 구조와 알고리즘 with C++을 기반으로 작성하였습니다>
알고리즘 및 이진 탐색
알고리즘
알고리즘(Algorithm)이란 주어진 문제를 해결하기 위한 일련의 명령들의 순서와 절차를 의미한다. 다시 말해, 문제를 정의하는 데 필요한 입력을 받아, 일련의 변환 과정을 거쳐 결과를 출력한다는 점에서 함수와 유사한 개념이다. 이러한 알고리즘은 문제를 효율적으로 해결하기 위해 설계되며, 이를 위해 다양한 최적화 기법이 사용된다.
알고리즘의 효율성은 해당 알고리즘의 동작과 수행에 필요한 명령 수에 따라 결정된다. 예를 들어 소수를 판별하는 알고리즘을 짰다고 가정하자.
// 소수 판별 알고리즘1
bool isPrime1(int n)
{
for (int i = 2; i < n; ++i)
{
if(n % i == 0)
return false;
}
return true;
}
// 소수 판별 알고리즘2
bool isPrime2(int n)
{
if (n <= 1)
return false;
if (n == 2 || n == 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i += 6)
{
if (n % i == 0 || n % (i + 2) == 0)
return false;
}
return true;
}두 개의 소수 판별 알고리즘 중 어떤 게 효율적일까? 먼저 첫 번째 함수는 2부터 n까지 모든 수를 확인하기 때문에 시간 복잡도가 O(n)이다. 두번째두 번째 함수는 반복문이 i = 5부터 시작하여 i * i <= n일 때까지 수행하며, i의 값은 반복문 내에서 6씩 증가하므로 대략 O(sqrt(n / 2))에 가깝다. 따라서 두 번째 함수가 더욱 효율적인 소수 판별 알고리즘이 되는 것이다.
따라서 우리는 효율적인 알고리즘을 짜는 것을 목표로 해야 한다.

이진 탐색 알고리즘
일반적인 검색 문제에 대해 고려해보자. 정렬되어 있는 정수 시퀀스가 있고, 여기에 숫자 N이 있는지 확인하려고 한다. 우리는 N을 찾기 위해 다음과 같이 코드를 작성하였다.
bool search(int n, std::vector<int>& v)
{
for(const auto& val : v)
{
if (val == N)
return true;
}
return false;
}이러한 시퀀스 전체 원소를 순회하면서 해당 원소가 N과 같은지를 확인하는 방법을 선형 검색(Linear search)라고 한다. 이 방법은 배열의 정렬 여부와 상관없이 항상 O(N)으로 잘 동작한다. 하지만 주어진 시퀀스가 정렬되어 있다는 점을 활용한다면 더 효율적인 알고리즘을 구현할 수 있다. 이러한 접근에서 나온 것이 바로 이진 탐색이다.
이진 탐색(Binary Search) 알고리즘은 정렬된 배열에서 원하는 값을 효율적으로 찾는 알고리즘 중 하나다. 탐색 방법은 다음과 같다.
- 배열의 중간 요소를 선택
- 중간 요소가 찾고자 하는 값과 일치하면 검색을 중단하고 해당 인덱스를 반환
- 찾고자 하는 값이 중간 요소보다 작으면, 중간 요소의 왼쪽 부분에서 탐색을 반복
- 찾고자 하는 값이 중간 요소보다 크다면, 중간 요소의 오른쪽 부분에서 탐색을 반복
- 원하는 값을 찾을 때까지 1-4를 반복
1부터 9까지 정수가 초기화된 배열 ary에 대해 2를 찾는 과정을 위의 이진 탐색 방법으로 찾아보자.
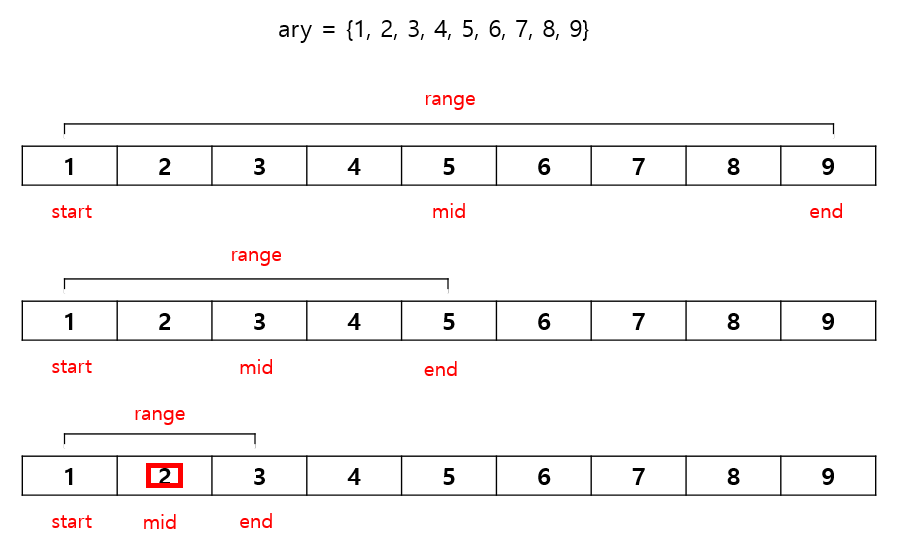
매 단계에서 탐색 범위가 절반씩 줄어들기 때문에 시간 복잡도가 O(logN)으로 선형 탐색보다 효율적이다. 따라서 대규모 데이터셋에 대해서도 빠른 탐색 속도를 보장한다. 물론 정렬 과정이 필요한 경우, 정렬에 따른 추가 시간 복잡도를 고려해야 하지만 대부분의 상황에서 선형 탐색보다 빠르다는 것이 보장된다.
구현
#include <iostream>
#include <vector>
bool binary_search(int n, std::vector<int>& v)
{
auto start = 0;
auto end = v.size() - 1;이진 탐색의 구현을 위해 binary_search() 함수를 작성해 보자. 이때 벡터 v는 정렬되어 있다고 가정하고, v내의 원소 중 n을 찾아 그 결괏값을 bool 값으로 리턴한다.
먼저 시작 위치 start, 마지막 위치 end를 초기화하자.
while (start <= end)
{
int mid = (start + end) / 2;
auto value = v[mid];
if (value == n)
return true;
else if (value < n)
start = mid + 1;
else
end = mid - 1;
}
return false;
}반복의 범위를 start와 end가 같거나 작아지는 시점으로 설정하고, 매 반복마다 중앙 인덱스와 그 위치의 값을 받아와 start와 end의 인덱스 값을 조정하면 된다.
int main()
{
std::vector<int> v = { 1,2,3,4,5,6,7,8,9 };
if (binary_search(2, v))
std::cout << "find the value\n";
else
std::cout << "cannot find the value\n";
}
이렇게 작성하고 출력하면 원하는 결과를 얻을 수 있다.
이론적으로 이진 탐색이 선형 탐색보다 더 효율적인 건 알았다. 하지만 그 차이를 가시적으로 얼마나 빠른지 확인해보고 싶다면 밑에 토글을 펼쳐서 확인해보자. 조금 어려울 수 있다.
작은 사이즈의 배열을 생성하여 찾아보고, 10만 개 이상의 수를 랜덤으로 생성하여 임의의 수를 찾아보자.
#include <iostream>
#include <vector>
#include <chrono>
#include <random>
bool linear_search(int n, std::vector<int>& v)
{
// 내용 같음
}
bool binary_search(int n, std::vector<int>& v)
{
// 내용 같음
}
void timeCheck(int n, std::vector<int>& v)
{
std::chrono::steady_clock::time_point begin, end;
std::chrono::microseconds diff;
begin = std::chrono::steady_clock::now();
if (linear_search(n, v))
std::cout << "Find the value " << n;
else
std::cout << "Cannot find the value " << n;
end = std::chrono::steady_clock::now();
diff = std::chrono::duration_cast<std::chrono::microseconds>(end - begin);
std::cout << " using linear search in " << diff.count() << "us\n";
begin = std::chrono::steady_clock::now();
if (binary_search(n, v))
std::cout << "Find the value " << n;
else
std::cout << "Cannot find the value " << n;
end = std::chrono::steady_clock::now();
diff = std::chrono::duration_cast<std::chrono::microseconds>(end - begin);
std::cout << " using binary search in " << diff.count() << "us\n";
}
int main()
{
std::vector<int> v = { 1,2,3,4,5,6,7,8,9 };
int n = 2;
// small size linear search
timeCheck(n, v);
// large size linear search
std::cout << std::endl; v.clear();
std::random_device rd;
std::mt19937 rand(rd());
std::uniform_int_distribution<std::mt19937::result_type> uniform_dist(1, 1000000);
for (int i = 0; i < 1000000; ++i)
v.push_back(uniform_dist(rand));
std::sort(v.begin(), v.end());
n = uniform_dist(rand);
timeCheck(n, v);
}
사이즈가 커질수록 수행하는 시간이 단축된다. 여기서 값을 찾지 못하는 것은 임의의 수를 벡터에 넣었기 때문에 배열 내에 원소가 없을 수 있으므로 크게 신경 쓰지 않아도 된다.
요약
알고리즘
- 주어진 문제를 해결하기 위한 일련의 명령들의 순서와 절차
이진 탐색
1. 정의: 정렬된 배열에서 원하는 값을 효율적으로 찾는 알고리즘
2. 탐색 방법
a. 배열의 중간 요소 선택
b. 중간 요소가 찾고자 하는 값과 일치하면 검색을 중단하고 해당 인덱스를 반환
c. 찾고자 하는 값이 중간 요소보다 작으면, 중간 요소의 왼쪽 부분에서 탐색을 반복
d. 찾고자 하는 값이 중간 요소보다 크다면, 중간 요소의 오른쪽 부분에서 탐색을 반복
e. 원하는 값을 찾을 때까지 a-d를 반복
3. 특징
a. 선형 탐색보다 효율적 (O(log(N))
b. 탐색 전에 정렬이 되어야 함
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘 - 개요 및 최단 작업 우선 스케줄링 (0) | 2023.05.22 |
|---|---|
| [알고리즘] 분할 정복 - 맵리듀스 (0) | 2023.05.20 |
| [알고리즘] 분할 정복 - 선형 시간 선택 (2) | 2023.05.19 |
| [알고리즘] 분할 정복 - 퀵 정렬 (0) | 2023.05.16 |
| [알고리즘] 분할 정복 - 병합 정렬 (2) | 2023.05.11 |