문제설명

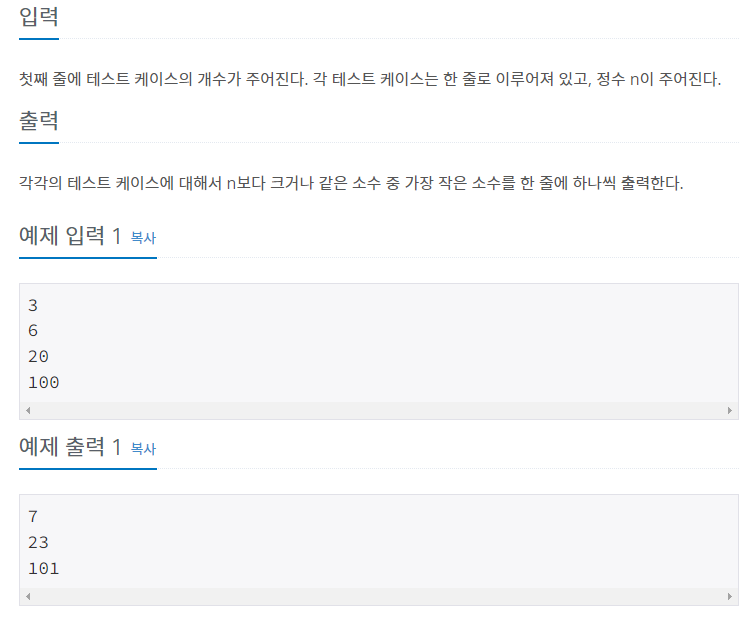
입출력 예제
개념
입력이 매우 클 때 소수를 찾는 문제다. 일반적인 O(N)의 시간 복잡도를 갖는 알고리즘은 시간 초과가 걸리기 때문에 효율적으로 소수를 구별해야 한다.
풀이
#include <iostream>
using namespace std;
int main()
{
long long N, n;
cin >> N;
for (int i = 0; i < N; ++i)
{
std::cin >> n;
while (!isPrime(n))
n++;
cout << n << endl;
}
}소수를 찾을 횟수 N을 초기화하고, 소수인지 구별할 정수 n을 초기화한다. n을 늘려가며 n보다 크지 않은 정수를 찾아 출력하게 구현하였다.
bool isPrime(long long num)
{
if (num <= 1)
return false;
if (num == 2 || num == 3)
return true;
if (num % 2 == 0 || num % 3 == 0)
return false;
for (long long i = 5; i * i <= num; ++i)
{
if (num % i == 0 || num % (i + 2) == 0)
return false;
}
return true;
}어떤 자연수 n이 소수가 아니라면 n은 p * q (p, q < n)의 형태로 나타낼 수 있다. 이때 p와 q 중 하나는 반드시 sqrt(n) 이하의 값을 가지고, 다른 하나는 sqrt(n) 이상의 값을 가진다.
- 이는 모순 증명으로 해결할 수 있는데, p와 q가 모두 sqrt(n)보다 크다고 가정하고 풀어보면 거짓이라는 것을 알 수 있다.
따라서 sqrt(n) 이하와 sqrt(n) 이상의 범위에 p와 q 중 하나가 존재하게 되므로 반복 범위를 i * i <= num으로 조절하여 시간 복잡도를 O(sqrt(n))으로 조절할 수 있다.
총합본
#include <iostream>
using namespace std;
bool isPrime(long long num)
{
if (num <= 1)
return false;
if (num == 2 || num == 3)
return true;
if (num % 2 == 0 || num % 3 == 0)
return false;
for (long long i = 5; i * i <= num; ++i)
{
if (num % i == 0 || num % (i + 2) == 0)
return false;
}
return true;
}
int main()
{
long long N, n;
cin >> N;
for (int i = 0; i < N; ++i)
{
std::cin >> n;
while (!isPrime(n))
n++;
cout << n << endl;
}
}'Algorithm > 백준' 카테고리의 다른 글
| [백준] 4948 베르트랑 공준 with C++ (0) | 2023.04.28 |
|---|---|
| [백준] 1929 소수 구하기 with C++ (0) | 2023.04.27 |
| [백준] 2485 가로수 with C++ (0) | 2023.04.25 |
| [백준] 1375 분수 합 with C++ (0) | 2023.04.24 |
| [백준] 13241 최소공배수 with C++ (0) | 2023.04.23 |