문제설명

입출력 예제

개념
심어져 있는 N개의 가로수 사이에 간격이 일정하도록 심어야 하는 가로수의 개수를 구하는 문제다. 이 문제를 해결하기 위해서 가로수들 사이의 거리를 구한 후, 거리를 일정하게 만들기 위해 최대 공약수 개념을 사용해야 한다.
풀이
#include <iostream>
#include <vector>
#include <numeric>
int main()
{
int N;
std::cin >> N;
std::vector<int> v(N);
std::vector<int> dist(N-1);
for (int i = 0; i < N; i++)
std::cin >> v[i];
for (int i = 1; i < v.size(); i++)
dist[i - 1] = v[i] - v[i - 1];가로수의 개수 N을 초기화하고, 가로수가 놓여 있는 위치를 초기화할 벡터 v, 가로수의 거리를 초기화할 벡터 dist를 초기화한다.
int gcd = std::accumulate(dist.begin(), dist.end(), dist[0], std::gcd<int, int>);
std::cout << (v.back() - v.front()) / gcd - (N - 1);
}거리의 최대 공약수를 std::accumulate() 함수를 이용해 구한다. 이 함수의 오버로딩을 보면 다음과 같다.
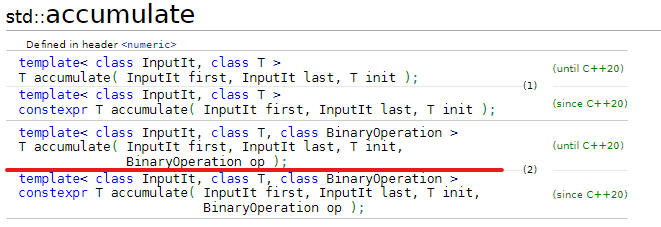
first부터 last까지 초깃값 Init을 op 연산을 이용해 더한다는 의민데, 여기에 gcd<>() 연산을 추가하여 주어진 배열 안에서의 최대 공약수를 구할 수 있다.
값을 다 구한 후, 가로수들 사이 간격을 최대 공약수로 나눠주고 1을 빼줘야 한다. 왜냐하면 양쪽에 이미 심어져 있으므로 하나를 빼줘야 결과가 올바르게 나오기 때문이다.
총합본
#include <iostream>
#include <vector>
#include <numeric>
int main()
{
int N;
std::cin >> N;
std::vector<int> v(N);
std::vector<int> dist(N-1);
for (int i = 0; i < N; i++)
std::cin >> v[i];
for (int i = 1; i < v.size(); i++)
dist[i - 1] = v[i] - v[i - 1];
int gcd = std::accumulate(dist.begin(), dist.end(), dist[0], std::gcd<int, int>);
std::cout << (v.back() - v.front()) / gcd - (N - 1);
}
반응형
'Algorithm > 백준' 카테고리의 다른 글
| [백준] 1929 소수 구하기 with C++ (0) | 2023.04.27 |
|---|---|
| [백준] 4134 다음 소수 with C++ (0) | 2023.04.26 |
| [백준] 1375 분수 합 with C++ (0) | 2023.04.24 |
| [백준] 13241 최소공배수 with C++ (0) | 2023.04.23 |
| [백준] 11478 서로 다른 부분 문자열의 개수 with C++ (0) | 2023.04.22 |