[임베디드] 신호와 주파수

<본 게시글은 "임베디드 레시피" 책을 기반으로 작성하였습니다>

---

Signal and Frequency

개요

시간 축의 펄스파(위)와 주파수 축의 펄스파(아래)

 

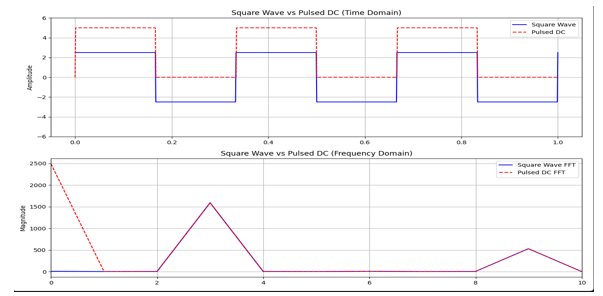
　임베디드 시스템은 다양한 신호를 처리하며, 센서로부터 입력된 데이터를 분석하고 필터링하여 제어 명령을 생성하기도 한다. 단적으로 오실로스코프로 측정하는 그래프도 신호의 일종이고, 수학 시간에 그렸던 함수들의 그래프도 신호의 일종이다. 이러한 신호에 대한 이해를 하는 것은 공학적인 측면에서 중요하다고 할 수 있다.

 

　이때 주파수는 새로운 시선을 제공한다. 시간 영역에서 복잡하게 보이는 신호도 주파수 영역으로 변환하면 단순한 주파수 성분들의 조합으로 분석할 수 있다. 이를 통해 신호의 성분을 쉽게 이해하고, 불필요한 노이즈를 제거하거나 원하는 주파수 대역을 강조할 수도 있다. 이번 시간에는 이러한 기초 개념을 중점적으로 다루어 보겠다.

---

본문

Signals

출처: 위키피디아

 

　신호(Signal)는 시간에 따라 변하는 물리적인 양을 의미한다. 임베디스 시스템에서는 아날로그 신호와 디지털 신호가 주로 사용된다.

 

　아날로그(Analog) 신호는 AC(교류)와 DC(직류)로 이루어진 연속적인 값을 갖는 신호를 의미한다. 여기서 교류는 극성이 바뀌는 신호를 의미하고, 직류는 극성이 바뀌지 않고 일정한 상태의 신호를 의미한다. 

• 즉, 교류는 전류나 전압이 시간이 지남에 따라 방향이 주기적으로 바뀌고, 직류는 전류나 전압이 일정한 방향으로만 흐르는 것을 의미

 

이산적인 펄스파(위), 노이즈가 추가된 펄스파(아래)

　

　디지털(Digital) 신호는 대부분 DC 성분으로 이루어진 0과 1의 이산적인 신호다. 이상적인 디지털 신호는 깨끗하게 0과 1로 구분되어 출력되는 것이 목표이지만, 실제 환경에서는 Bounce라고 불리는 노이즈가 끼어 신호가 불안정해질 수 있습니다. 이러한 노이즈로 인해 위의 그래프와 같이 신호가 이상적으로 표현되지 않고, 특정 구간에서 값이 불규칙하게 흔들리는 현상이 발생한다.

 

　만약 실제 통신 과정에서 이러한 노이즈가 발생한다면 임계값(Threshold)을 이용해 이를 기준으로 1과 0을 나누면 된다. 하지만 위의 그래프와 같이 노이즈가 심해 그 임계값을 넘어버리면 신호가 왜곡되어 원하는 출력과 결과가 달라지는 상황이 발생한다. 이를 해결하기 위해 우리는 주파수를 사용한다.

---

Frequency

출처: 삼성반도체이야기

 

　주파수(Frequency)는 사전적으로 진동운동에서 단위 시간당 같은 것이 일어난 횟수를 의미한다. 만약 3Hz의 주파수를 갖는다고 하면, 1초 동안 동일한 진동이 세 번 일어난다는 것을 의미하고, 주기는 주파수의 역수인 333ms가 된다. 

 

출처: 위키피디아

 

　이런 주파수는 푸리에 트랜스폼(Fourier Transform)을 이용해 새로운 관점에서 문제를 해석할 때 중요한 역할을 한다. 해당 개념은 쉽게 생각해서 모든 신호는 여러 개의 주기 함수의 합으로 나타낼 수 있으며, 이는 곧 시간 축에서의 신호를 주파수 별로 분리해 준다는 것이다. 

• 푸리에 트랜스폼에 대한 설명은 해당 글에서 설명했으니 참조하도록 하자.

 

 

　해당 노이즈 신호를 예로 들어보자. 이를 시간 축에서 노이즈를 필터링하려니 쉽지 않아 보인다. 하지만 이를 주파수 축으로 바꿔(Fourier Transform을 적용) 보면 다음과 같이 나온다. 이해하기 쉽게 노이즈가 타지 않은 깨끗한 신호와 비교해서 표시했다.

 

 

　해당 그래프를 보면, 노이즈가 탄 신호가 원래 신호와 비교해서 고주파수 성분이 많은 것을 알 수 있다. 일반적으로 노이즈는 고주파수 성분이기 때문에, 해당 부분에 필터를 씌우고, 임계값을 기준으로 0과 1로 이진화하면 신호를 복원할 수 있다.

 

 

　사실 신호와 주파수는 굉장히 복잡하고 어려운 내용이다. 하지만 임베디드 시스템을 이해하는 관점에서는 위와 같이 간략한 개념정도만 파악하고 있으면 큰 어려움은 없을 것으로 예상한다. 혹시 위와 같은 그래프를 그려낸 과정이 궁금하면 아래 접은 글을 확인하면 된다.

 

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, ifft

# 0과 1로 이루어진 펄스파 생성
t = np.linspace(0, 1, 500, endpoint=False)
pulse_wave = np.where((t >= 0.4) & (t < 0.6), 1, 0)

# 노이즈 추가
noise = np.random.normal(0, 0.2, pulse_wave.shape)
noisy_signal = pulse_wave + noise

# 푸리에 변환 (FFT)
fft_signal = fft(noisy_signal)
fft_pulse = fft(pulse_wave)

# 주파수 성분 필터링 (고주파 제거)
freqs = np.fft.fftfreq(len(t), d=t[1] - t[0])
fft_filtered = np.where(np.abs(freqs) < 50, fft_signal, 0)

# 역 푸리에 변환 (IFFT)
recovered_signal = ifft(fft_filtered)

# 복원된 신호를 0.5 기준으로 0과 1로 이진화
binary_signal = np.where(recovered_signal.real >= 0.5, 1, 0)

# 그래프 그리기
plt.figure(figsize=(12, 12))

plt.subplot(6, 1, 1)
plt.plot(t, pulse_wave)
plt.title("Original Pulse Wave")

plt.subplot(6, 1, 2)
plt.plot(t, noisy_signal)
plt.title("Noisy Signal")

plt.subplot(6, 1, 3)
plt.plot(freqs[:len(freqs)//2], np.abs(fft_pulse[:len(freqs)//2]))
plt.title("Original Pulse Wave Frequency Spectrum")

plt.subplot(6, 1, 4)
plt.plot(freqs[:len(freqs)//2], np.abs(fft_signal[:len(freqs)//2]))
plt.title("Noisy Signal Frequency Spectrum")

plt.subplot(6, 1, 5)
plt.plot(t, recovered_signal.real)
plt.title("Recovered Signal after Filtering")

plt.subplot(6, 1, 6)
plt.plot(t, binary_signal)
plt.title("Binary Signal (Thresholded at 0.5)")

plt.tight_layout()
plt.show()

---

 

요약

신호: 시간에 따라 변하는 물리적인 양
아날로그 신호: 연속적인 신호
디지털 신호: 0과 1로 이루어진 이산적인 신호
AC(교류): 극성이 바뀌는 신호
DC(직류): 극성이 바뀌지 않는 신호

주파수: 단위 시간당 같은 것이 일어난 횟수
주기: 한 번 진동하는 데 걸리는 시간 (주파수의 역수)
푸리에 변환: 시간 축의 정보를 주파수 축의 정보로 변환
-> 모든 신호는 여러 개의 주기 함수의 합으로 나타낼 수 있음