문제설명
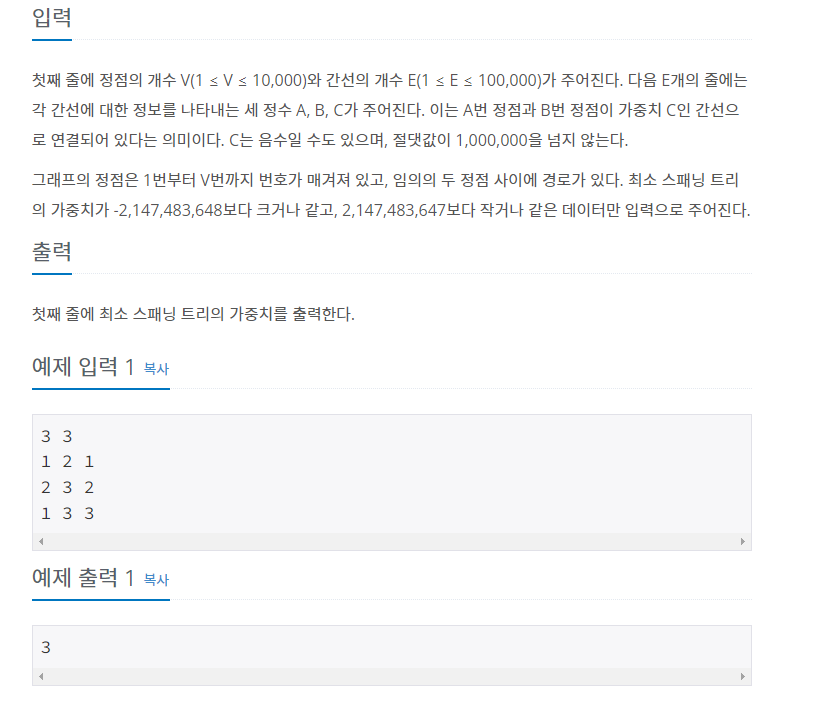
입출력 예제
개념
최소 신장 트리 문제다. 주어진 그래프에서 가중치의 합이 최소가 되는 트리를 찾는 것이므로, MST 알고리즘 중 크루스칼 알고리즘을 이용해서 풀면 해결할 수 있다. 이때 Kruskal 알고리즘은 모든 간선들의 가중치를 오름차순으로 정렬하고, 가장 가중치가 작은 간선부터 연결해 나가면서 MST를 만들어 나가는 알고리즘이다.
풀이
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int findParent(int parent[], int node)
{
while (parent[node] != node)
node = parent[node];
return node;
}
void unionParent(int parent[], int a, int b)
{
a = findParent(parent, a);
b = findParent(parent, b);
if (a < b)
parent[b] = a;
else
parent[a] = b;
}크루스칼 알고리즘의 핵심인 Union-Find 알고리즘이다. 이는 그래프에서 사이클을 찾거나, Disjoint-set을 관리하는 데 사용된다. 여기서 findParent 함수는 그래프의 노드가 어떤 트리에 속해있는지 알려주는 역할을 한다. 만약 같은 집합에 속해 있다면, 그 두 노드를 잇는 간선은 사이클을 형성한다는 것을 알 수 있다.
unionParent() 함수는 두 트리를 하나로 합치는 역할을 한다. 간선으로 두 노드를 잇고자 할 때, 두 노드가 서로 다른 집합에 속해 있다면 그 두 집합을 하나로 합치는 연산이다. 이를 통해 두 노드를 안전하게 잇는 것이 가능하며, 이 과정이 반복되면 모든 노드가 하나의 트리가 된다.
int main()
{
ios_base::sync_with_stdio(false); cout.tie(nullptr); cin.tie(nullptr);
vector<pair<int, pair<int, int>>> edge;
int V, E, a, b, c, res = 0;
cin >> V >> E;
int* parent = new int[V + 1];
for (int i = 1; i <= V; ++i)
parent[i] = i;정점의 개수 V+1만큼 부모 노드 parent를 생성한다. 이때 초기에는 각 노드가 자기 자신을 부모로 가진다.
for (int i = 0; i < E; ++i)
{
cin >> a >> b >> c;
edge.push_back({ c, {a,b} });
}
sort(edge.begin(), edge.end());간선의 정보를 가중치, {노드1, 노드2}의 형태로 저장하고 가중치 기준으로 간선을 정렬한다.
for (int i = 0; i < E; ++i)
{
int weight = edge[i].first;
a = edge[i].second.first;
b = edge[i].second.second;
if (findParent(parent, a) != findParent(parent, b))
{
unionParent(parent, a, b);
res += weight;
}
}
cout << res;
}모든 간선에 대해 간선의 한 끝 노드 a와 다른 끝 노드 b를 비교한다. findParent() 함수를 통해 각 노드의 루트를 찾고, 이 두 노드가 같은 집합에 속해 있지 않다면 a와 b를 unionParent() 함수를 이용해 합친다. 그리고 해당 간선의 가중치를 결과에 더하면 된다.
총합본
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int findParent(int parent[], int node)
{
while (parent[node] != node)
node = parent[node];
return node;
}
void unionParent(int parent[], int a, int b)
{
a = findParent(parent, a);
b = findParent(parent, b);
if (a < b)
parent[b] = a;
else
parent[a] = b;
}
int main()
{
ios_base::sync_with_stdio(false); cout.tie(nullptr); cin.tie(nullptr);
vector<pair<int, pair<int, int>>> edge;
int V, E, a, b, c, res = 0;
cin >> V >> E;
int* parent = new int[V + 1];
for (int i = 1; i <= V; ++i)
parent[i] = i;
for (int i = 0; i < E; ++i)
{
cin >> a >> b >> c;
edge.push_back({ c, {a,b} });
}
sort(edge.begin(), edge.end());
for (int i = 0; i < E; ++i)
{
int weight = edge[i].first;
a = edge[i].second.first;
b = edge[i].second.second;
if (findParent(parent, a) != findParent(parent, b))
{
unionParent(parent, a, b);
res += weight;
}
}
cout << res;
}
'Algorithm > 백준' 카테고리의 다른 글
| [백준] 8979 올림픽 with C++ (0) | 2023.06.25 |
|---|---|
| [백준] 1026 보물 with C++ (0) | 2023.06.23 |
| [백준] 9372 상근이의 여행 with C++ (0) | 2023.06.16 |
| [백준] 1655 가운데를 말해요 with C++ (0) | 2023.06.14 |
| [백준] 13305 주유소 with C++ (0) | 2023.06.11 |