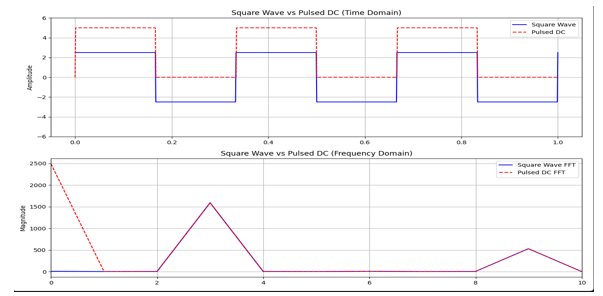
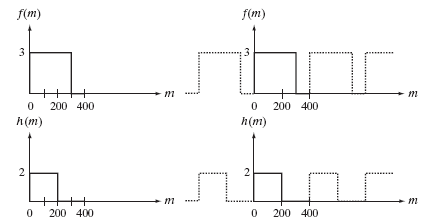
임베디드 레시피" 책을 기반으로 작성하였습니다>Signal and Frequency개요 임베디드 시스템은 다양한 신호를 처리하며, 센서로부터 입력된 데이터를 분석하고 필터링하여 제어 명령을 생성하기도 한다. 단적으로 오실로스코프로 측정하는 그래프도 신호의 일종이고, 수학 시간에 그렸던 함수들의 그래프도 신호의 일종이다. 이러한 신호에 대한 이해를 하는 것은 공학적인 측면에서 중요하다고 할 수 있다. 이때 주파수는 새로운 시선을 제공한다. 시간 영역에서 복잡하게 보이는 신호도 주파수 영역으로 변환하면 단순한 주파수 성분들의 조합으로 분석할 수 있다. 이를 통해 신호의 성분을 쉽게 이해하고, 불필요한 노이즈를 제거하거나 원하는 주파수 대역을 강조할 수도 있다. 이번 시간에는 이러한 기초 개념을 중점적으로..