<본 카테고리는 "코딩 테스트를 위한 자료 구조와 알고리즘 with C++을 기반으로 작성하였습니다>
그래프(Graph)
개요
지금까지 공부한 트리는 계층적인 데이터를 표현하기에 적합한 자료구조지만, 원형 또는 순환적인 종속성을 표현할 수 없다. 예를 들어 서울과 광역시간의 이동 정보를 생각해 보면, 특정 장소에서 다른 장소로 이동하기 위한 다양한 경로가 존재할 수 있다. 이러한 경우엔 노드와 간선(edge)을 모아놓은 자료구조인 그래프를 사용하는 것이 더 적합하다. 그래프는 순환 구조를 가지므로, 이러한 경우에도 경로를 표현할 수 있다. 따라서, 계층적인 데이터가 아닌 경우엔 그래프를 사용하는 것이 더욱 유용할 것이다.
종류
그래`프는 다양한 종류가 있으며, 먼저 무방향(Undirected) 그래프와 방향(Directed) 그래프로 나뉜다. 무방향 그래프에서는 간선이 양방향으로 연결되어 있으며, 방향 그래프에서는 간선이 단방향으로 연결된다.
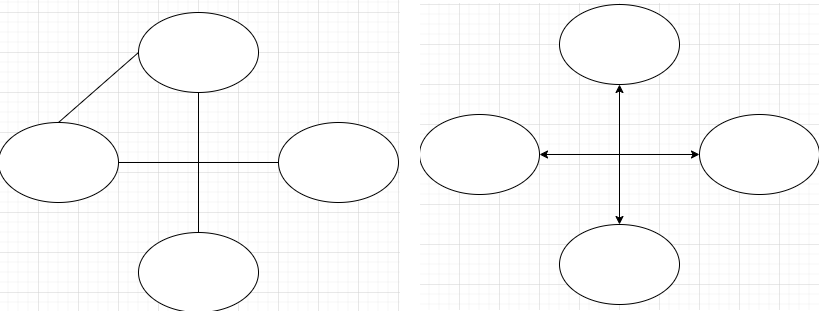
또한 에지에 가중치를 부여하는 가중(Weighted) 그래프와 비가중(Unweighted) 그래프로 나뉜다. 즉, 노드 데이터뿐만 아니라 노드 사이의 에지 데이터도 저장하는 것을 의미한다.
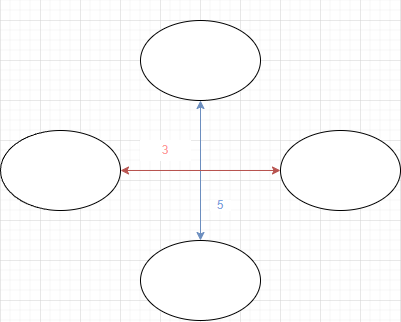
구현
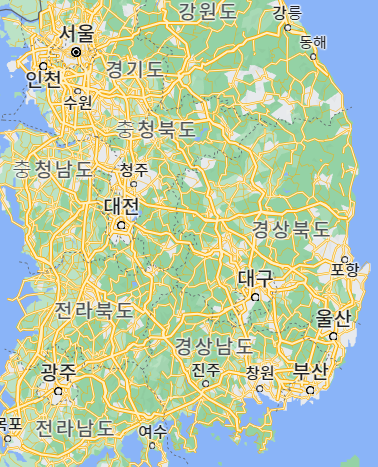
위의 사진은 대한민국의 지도다. 임의로 특별시와 광역시의 이동 정보를 다음과 같이 나타낼 수 있다고 가정해보자.

이를 배열에서 특정 원소가 해당 원소 인덱스에 해당하는 노드 사이의 가중치를 표현하는 인접(Adjacency) 행렬 방식과 각 노드에 직접 연결되어 있는 노드의 ID만 저장하는 방식인 인접 리스트로 구현해 보겠다.
인접 행렬 방식
#include <iostream>
#include <vector>
enum class city : int
{
SEOUL,
INCHEON,
DAEJEON,
GWANGJU,
DAEGU,
BUSAN,
ULSAN
};enum 클래스를 이용하여 도시 이름을 저장한다. 이때 enum과 enum클래스의 차이는 다음과 같다.
- enum: 별도의 이름 공간이 존재하지 않음
- enum class: 범위 연산자 '::'를 이용하여 쉽게 접근 가능
std::ostream& operator << (std::ostream& os, const city c)
{
switch (c)
{
case city::SEOUL:
os << "서울";
return os;
case city::INCHEON:
os << "인천";
return os;
case city::DAEJEON:
os << "대전";
return os;
case city::GWANGJU:
os << "광주";
return os;
case city::DAEGU:
os << "대구";
return os;
case city::BUSAN:
os << "부산";
return os;
case city::ULSAN:
os << "울산";
return os;
default:
return os;
}
}enum city에 대해 << 연산자를 재정의하여 원하는 문자열이 출력되게 설정한다.
class graph
{
std::vector<std::vector<int>> _graph;
public:
graph(int n)
{
_graph.reserve(n);
std::vector<int> row(n, -1);
for (int i = 0; i < n; i++)
_graph.push_back(row);
}그래프 클래스를 생성한다. 여기서 2차원을 표현해야 하므로 vector를 vector<vector<>> 꼴로 초기화한다.
void addEdge(const city c1, const city c2, int weight)
{
std::cout << "에지 추가: " << c1 << '-' << c2 << '=' << weight << '\n';
int n1 = static_cast<int>(c1);
int n2 = static_cast<int>(c2);
_graph[n1][n2] = weight;
_graph[n2][n1] = weight;
}
void removeEdge(const city c1, const city c2)
{
std::cout << "에지 삭제: " << c1 << '-' << c2 << '\n';
int n1 = static_cast<int>(c1);
int n2 = static_cast<int>(c2);
_graph[n1][n2] = -1;
_graph[n2][n1] = -1;
}
};간선을 추가하는 함수와 삭제하는 함수를 작성한다. 이때 _graph[n1][n2], _graph[n2][n1] 모두 값을 할당하는 이유는 위의 지도에서 이동 정보가 양방향이기 때문이다.
int main()
{
graph Korea(7);
Korea.addEdge(city::SEOUL, city::INCHEON, 9000);
Korea.addEdge(city::SEOUL, city::DAEJEON, 8000);
Korea.addEdge(city::SEOUL, city::DAEGU, 5000);
Korea.addEdge(city::INCHEON, city::DAEJEON, 7000);
Korea.addEdge(city::DAEJEON, city::GWANGJU, 5000);
Korea.addEdge(city::DAEJEON, city::DAEGU, 0);
Korea.addEdge(city::GWANGJU, city::DAEGU, 2000);
Korea.addEdge(city::GWANGJU, city::BUSAN, 1000);
Korea.addEdge(city::DAEGU, city::BUSAN, 5000);
Korea.addEdge(city::DAEGU, city::ULSAN, 2000);
Korea.addEdge(city::BUSAN, city::ULSAN, 3000);
Korea.removeEdge(city::DAEGU, city::DAEJEON);
}마지막으로 main 함수에서 간선을 추가해 주면 된다.

인접 리스트 방식
#include <iostream>
#include <algorithm>
#include <vector>
enum class city : int
{
SEOUL,
INCHEON,
DAEJEON,
GWANGJU,
DAEGU,
BUSAN,
ULSAN
};
std::ostream& operator << (std::ostream& os, const city c)
{
switch (c)
{
case city::SEOUL:
os << "서울";
return os;
case city::INCHEON:
os << "인천";
return os;
case city::DAEJEON:
os << "대전";
return os;
case city::GWANGJU:
os << "광주";
return os;
case city::DAEGU:
os << "대구";
return os;
case city::BUSAN:
os << "부산";
return os;
case city::ULSAN:
os << "울산";
return os;
default:
return os;
}
}enum class와 연산자 오버로딩은 동일하게 작성해 준다.
class graph
{
std::vector<std::vector<std::pair<int, int>>> _graph;
public:
graph(int n)
{
_graph = std::vector<std::vector<std::pair<int, int>>>(n,
std::vector<std::pair<int, int>>());
}vector와 pair를 이용해 노드를 표현하고 있는데, _graph[0]부터 _graph[6]까지는 각각 서울부터 울산을 의미하게 된다.
void addEdge(const city c1, const city c2, int weight)
{
std::cout << "에지 추가: " << c1 << '-' << c2 << '=' << weight << '\n';
int n1 = static_cast<int>(c1);
int n2 = static_cast<int>(c2);
_graph[n1].push_back({ n2, weight });
_graph[n2].push_back({ n1, weight });
}
void removeEdge(const city c1, const city c2)
{
std::cout << "에지 삭제: " << c1 << '-' << c2 << '\n';
int n1 = static_cast<int>(c1);
int n2 = static_cast<int>(c2);
std::remove_if(_graph[n1].begin(), _graph[n1].end(), [n2](const auto& pair)
{
return pair.first == n2;
});
std::remove_if(_graph[n2].begin(), _graph[n2].end(), [n1](const auto& pair)
{
return pair.first == n1;
});
}
};노드를 추가하고 삭제하는 메서드들이다. 만약 _graph[n1].push_back({ n2, weight}); 가 실행되면 n1과 n2가 연결되며 가중치가 weight로 설정된다.
반대로 std::remove_if() 함수가 실행되면, 입력된 노드 번호에 해당하는 정점과 연결된 모든 간선 중에서 지우고자 하는 노드 번호에 해당하는 간선을 찾은 후, 이를 지운다.
int main()
{
graph Korea(7);
Korea.addEdge(city::SEOUL, city::INCHEON, 9000);
Korea.addEdge(city::SEOUL, city::DAEJEON, 8000);
Korea.addEdge(city::SEOUL, city::DAEGU, 5000);
Korea.addEdge(city::INCHEON, city::DAEJEON, 7000);
Korea.addEdge(city::DAEJEON, city::GWANGJU, 5000);
Korea.addEdge(city::DAEJEON, city::DAEGU, 0);
Korea.addEdge(city::GWANGJU, city::DAEGU, 2000);
Korea.addEdge(city::GWANGJU, city::BUSAN, 1000);
Korea.addEdge(city::DAEGU, city::BUSAN, 5000);
Korea.addEdge(city::DAEGU, city::ULSAN, 2000);
Korea.addEdge(city::BUSAN, city::ULSAN, 3000);
Korea.removeEdge(city::DAEGU, city::DAEJEON);
}메인 함수에 다음과 같이 작성하면 인접 배열과 똑같은 방식으로 결과가 출력된다는 것을 알 수 있다.
인접 배열 vs 인접 리스트
인접 배열은 벡터의 벡터를 이용하여 데이터를 저장했고, 각 벡터의 크기는 노드 개수와 같다. 따라서 노드 개수가 n이라면, n * n 크기의 메모리 공간을 사용하게 된다. 반대로 인접 리스트는 각 노드에 인접한 노드를 리스트로 저장하기 때문에 안쪽 벡터의 크기가 해당 노드에 연결된 노드 개수와 같다. 따라서 에지 개수 n에 비례한 크기의 메모리를 사용하게 된다.
만약 간선의 개수가 적은 그래프의 경우엔 메모리 사용량을 줄일 수 있고 시간 복잡도가 낮은 인접 리스트를 사용하고, 간선의 개수가 많다면 그래프의 크기가 큰 경우에도 빠르게 간선의 연결 여부를 확인할 수 있는 인접 행렬이 적합하다.
요약
그래프
1. 정의: 노드와 간선을 모아놓은 자료구조
2. 종류
a. 무방향 그래프, 방향 그래프
b. 가중 그래프, 비가중 그래프
3. 구현
a. 인접 배열: 간선의 개수가 많을 때
b. 인접 리스트: 간선의 개수가 적을 때
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 해시 테이블 (2) (0) | 2023.04.27 |
|---|---|
| [자료구조] 해시 테이블 (1) (0) | 2023.04.26 |
| [자료구조] 힙 (2) | 2023.04.20 |
| [자료구조] 이진 탐색 트리 (2) - 구현 (0) | 2023.04.20 |
| [자료구조] 이진 탐색 트리 (1) (0) | 2023.04.19 |