<본 글은 레트로의 유니티 게임 프로그래밍 에센스(개정판)를 참고로 하여 작성하였습니다>
유니티 C# 벡터
Vector type
앞선 [유니티] 방향, 크기, 회전 (1) 포스트에서는 수학적 의미에서 벡터를 다루었다. 이번 게시글에서는 게임 개발에 필요한 기본적인 벡터 수학을 유니티 C#에 적용하는 방법을 알아보자.
유니티는 벡터를 표현하기 위해 Vetor2, Vector3, Vector4를 제공하고 있다. 가장 많이 사용할 Vector3의 정의를 보기 위해 유니티 공식 홈페이지에 접속해 보면 다음과 같이 설명하고 있다.

이때 주목해야할 점은 Vector 타입이 구조체(struct)로 선언되어 있다는 점이다. 클래스로 선언하지 않고 구조체를 이용한 이유는 값 타입으로 동작하게 하여 복사를 했을 때 수정되는 것을 막기 위해서다. 직관적으로 이해하기 위해 다음 예제를 보도록 하자.
Vector3 a = new Vector3(0,0,0);
Vector3 b = a;
b.x = 100;다음과 같이 (0,0,0) 의 값을 가지는 벡터 a가 선언되었고, 이 값을 그대로 b 값이 갖게 하였다고 하자. 그 후에 b의 x값을 100으로 수정하였다. 만약 Vector3가 클래스 타입으로 선언되었다면 참조 타입으로 동작하므로 a와 b 모두 (100, 0, 0)이라는 값을 가질 것이다.
하지만 유니티에서는 Vector 타입을 구조체로 선언하였기 때문에 a는 (0, 0, 0), b는 (100, 0, 0)으로 다른 값을 가지게 된다.
Vector Operation
앞선 포스팅에서 배웠던 스칼라 곱, 덧셈과 뺄셈, 내적과 외적, 정규화, 크기 모두 구현되어 있다. 다음 예제를 통해 벡터의 연산을 구현해 보자.
Vector3 va = new Vector3 (3, 6, 9);
Vector3 vb = new Vector3 (2, 4, 6);
// 덧셈 뺄셈
Vecotr3 vc = va + vb; // (5, 10, 15)
vc = va - vb // (1, 2, 3)
// 정규화, 크기
va.normalized; // (0.27, 0.53, 0.80)
va.magnitude; // 11.22
// 내적, 외적
va = (0, 1, 0);
vb = (1, 0, 0);
float c = Vector3.Dot(va, vb); // 수직인 벡터끼리의 내적이므로 0
vc = Vector3.Cross(va, vb); // x와 y의 외적이므로 (0, 0, 1)
그렇다면 이러한 벡터 연산을 응용해 보자. 앞선 게시글에서 벡터의 뺄셈을 통해 두 벡터 사이의 간격을 구할 수 있다고 하였다. 그리고 이를 이용해 물체를 추적할 때 어떤 방향으로 얼마만큼 가야 하는지 알 수 있다고 하였다.
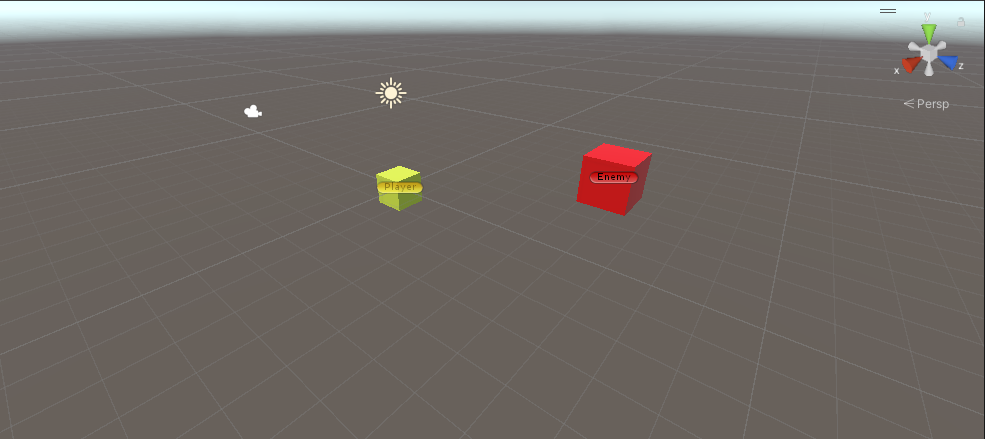
예를 들어보자. 플레이어가 타깃을 공격하려고 하면, 타깃과 플레이어 사이의 방향을 알아야 한다. 그렇다면 플레이어의 위치와 타깃의 위치를 뺀 다음 정규화하면 그 방향벡터를 구할 수 있지 않을까? 다음과 같이 코드를 짜고 콘솔창을 보면 우리의 예상이 맞다는 것을 알 수 있다.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class example : MonoBehaviour
{
public Transform player, target;
Vector3 currnetPos;
Vector3 targetPos;
void Start()
{
currnetPos = player.transform.position;
targetPos = target.transform.position;
Debug.Log("방향 벡터: " + (targetPos - currnetPos).normalized);
}
}
Quaternion
유니티에서 트랜스 컴포넌트의 회전 타입은 Vector3가 아니라 쿼터니언으로 지정되어 있다. 여기서 쿼터니언(Quaternion)이란 회전을 나타내는 타입으로서, x, y, z, w를 가지는 값으로 사원수라고도 부른다. 일반적인 3D 벡터로 다루지 않고 쿼터니언을 다루는 이유를 이해하기 위해선 3D 벡터의 한계점인 짐벌락을 이해해야 한다.
쿼터니언으로 다루지 않고 3D 벡터를 사용해 회전을 나타내는 표현을 오일러각(Euler angle)이라고 한다. 오일러가 고안한 이 방법은 회전하기 전 상태에서 회전한 다음 상태를 표현하기 위해 x, y, z에 대해 각각 얼마만큼 회전하면 되는지 계산한다. 따라서 회전을 한 번에 계산하지 않고, 세 번에 거쳐 계산하기 때문에 축이 겹치는 문제가 발생할 수 있다.
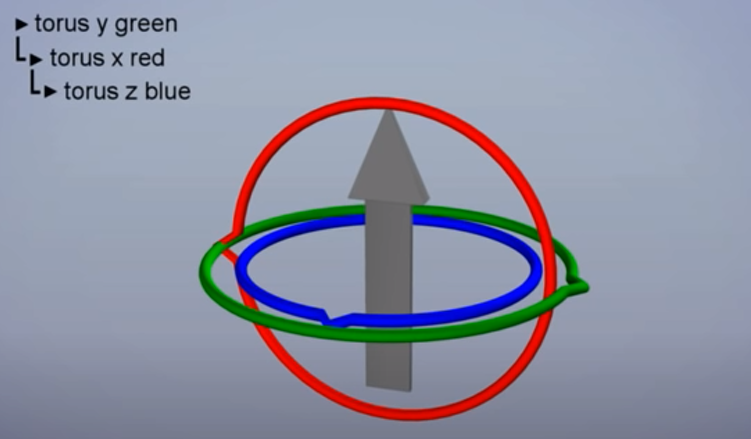
즉, 짐벌락(Gimbal lock)이란 두 번의 회전에 의해 세 번째 회전의 자유도가 상실되어 세 축 중 한 축의 회전을 사용할 수 없게 되는 현상을 의미한다. 이런 현상에 의해 오일러각으로 회전을 표현하는 방식에는 문제가 있다는 것을 알 수 있다. (과거에는 이런 현상을 방지하기 위해 90도 회전을 하지 않고 89.9xx 도 같은 값으로 회전을 처리했음)
이러한 문제점을 해결하기 위해 등장한 것이 바로 쿼터니언 방식이다. 쿼터니언은 한 번에 회전하는 방식이기 때문에 짐벌락 문제가 발생하지 않고, 만일 행렬을 사용해 회전할 경우에도 행렬의 합성을 통해 해결할 수도 있다. 하지만 쿼터니언의 선형 대수적 원리를 이해하지 못하면 직관적이지 않다는 단점이 존재한다. 따라서 유니티 내부에선 회전을 쿼터니언으로 처리하지만, 우리가 눈으로 보는 인스펙터 창에서는 오일러각으로 다루고 있다.

요약
Vector type
1. 정의: 유니티에서 벡터를 처리하는 자료형
2. 특징
a. 구조체로 정의되어 있어 값으로 처리함
b. 우리가 알고 있는 벡터 연산이 가능함
Quaternion
1. 정의: 회전을 나타내는 타입으로서, x, y, z, w를 가지는 값으로 사원수
2. 특징
a. 기존의 오일러각(Euler Angle) 방식에서 발생했던 짐벌락(Gimbal Lock) 현상을 일으키지 않음
b. 회전이 한 번에 이루어짐
c. 직관적이지 않음
'Game > Unity' 카테고리의 다른 글
| [유니티] 글자 하나씩 출력하기 (0) | 2023.04.30 |
|---|---|
| [유니티] 오브젝트 풀링(Object Pooling) (0) | 2023.04.13 |
| [유니티] 방향, 크기, 회전 (1) (0) | 2023.02.15 |
| [유니티] 유니티 엔진 원리 (0) | 2023.02.09 |
| [유니티] 프리팹(Prefabs)과 감지(Detection), 충돌(Collision) (2) (0) | 2023.02.01 |